– à partir de son expression algébrique
f(x)=2x^3+2
– sa représentation graphique :
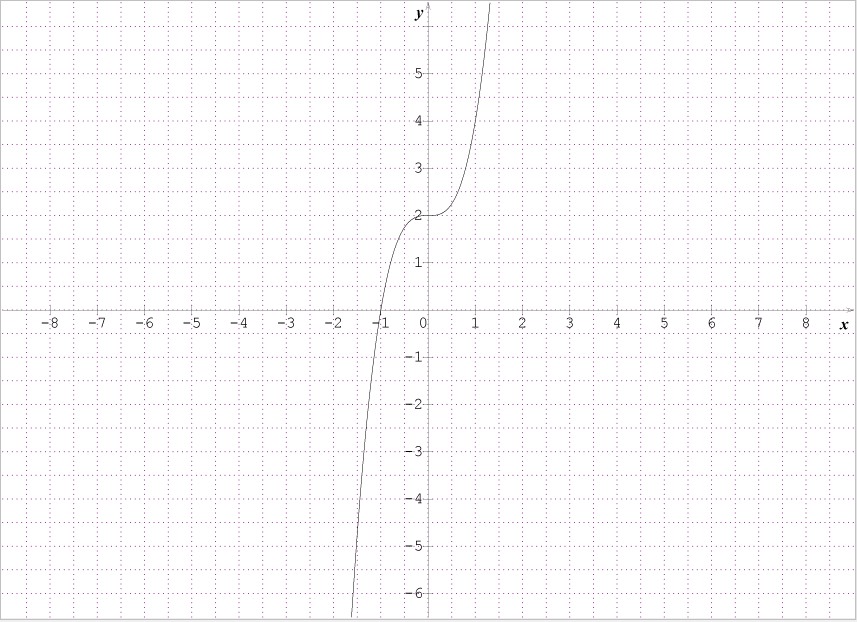
– et son tableau de valeurs :
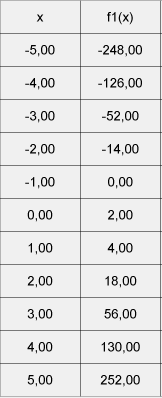
Prenons ce rugbyman qui tape dans un ballon :

Plusieurs trajectoires sont possibles :

La trajectoire peut être modélisée par une fonction numérique. Cette année, nous allons pouvoir prévoir les variations de la fonction numérique (ici la trajectoire).
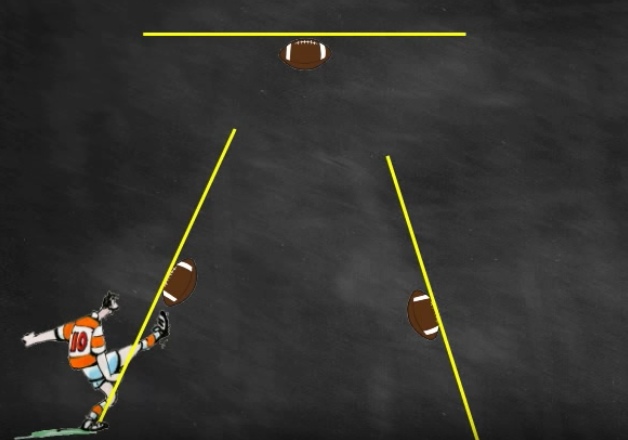
On va s’aider des tangentes en plusieurs points à la trajectoire du ballon.
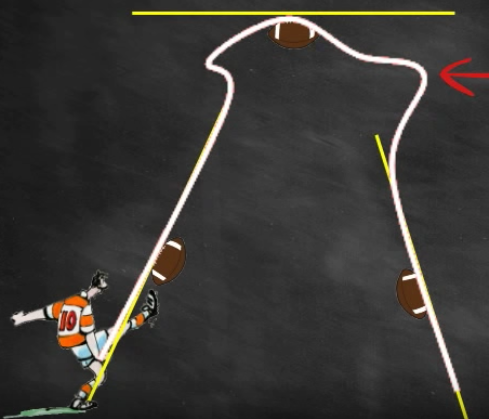
Pour être plus précis, on va multiplier les points de la trjectoire…

et calculer les tangentes.
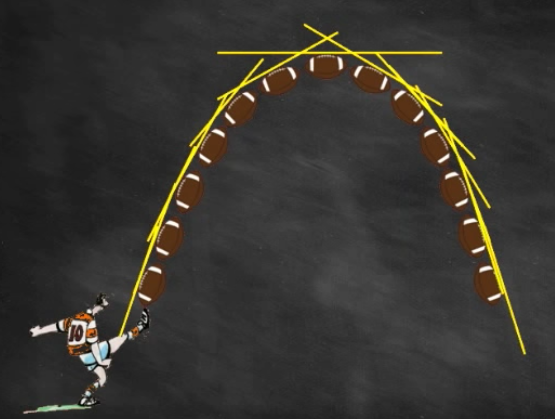
On a donc réussi à affiner la trajectoire du ballon.
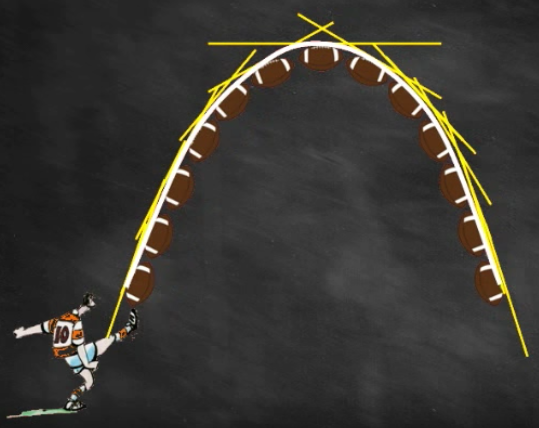
Les tangentes sont intéressantes car ce sont des droites donc faciles à étudier en mathématiques.
Les droites,représentations graphiques, ont été étudiées en seconde par leur fonction, la fonction affine f(x)=ax+b.
Une droite se caractérise avant tout par son coefficient directeur a qui nous indique si la droite est croissante ou décroissante.
Revenons une dernière fois sur notre rugbyman :
On voit que les tangentes ont un coefficient directeur positif quand la trajectoire monte et qu’elles ont un coefficient directeur négatif quand la trajectoire descend.
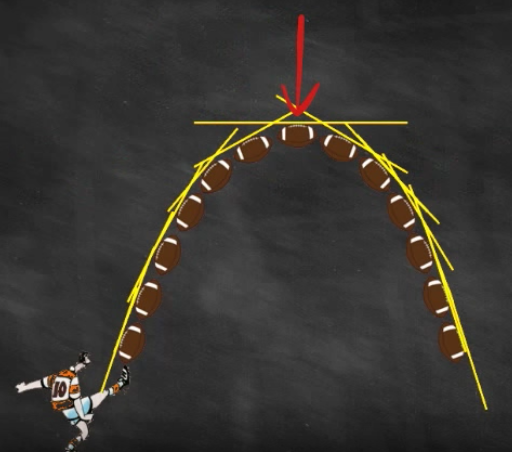
De plus lorsqu’on arrive au sommet de la trajectoire, le coefficient directeur de la tangente parallèle au sol (axe des abscisses) est nul.
– signe positif : trajectoire croissante
– signe nul : trajectoire constante
– signe négatif : trajectoire décroissante
C’est ce coefficient directeur de tangente que l’on appellera maintenant le nombre dérivé.
Il y autant de nombres dérivées que de tangentes possibles en chaque point de la courbe.
L’ensemble des nombres dérivés sont obtenus grâce à la fonction dérivée de la fonction numérique étudiée.
x \mapsto f'(x)
On dit « f prime de x ».