Archives de catégorie : Fonction dérivée et étude des variations d’une fonction
FD10 – Troisième problème
Le coût de production C(n) exprimé en milliers d’euro pour n articles est donné par la fonction C avec : C(n)=0,02n^2-2n+98 pour n appartenant à l’intervalle [50 ; 150].
Le montant des ventes V(n) exprimé en milliers d’euro est pour sa part donné par la fonction V avec V(n)=1,5n pour n appartenant à l’intervalle [50 ; 150].
| n | 50 | 60 | 75 | 90 | 100 | 125 | 150 |
| C(n) | … | 50 | … | … | 98 | … | 248 |
C(75)=60,5
C(90)=80
C(125)=160,5
Exprimer B(n) en fonction de n et déterminer la dérivée B'(n).
B(n)==1,5n-(0,02n^2-2n+98)
B(n)=-0,02n^2+3,5n-98
B'(n)=-0,04n+3,5
-0,04n+3,5=0
-0,04n=-3,5
n=87,5
Le nombre d’article est maximum pour n=87,5 car la fonction B est une fonction carrée et sa dérivée change de signe en n=87,5.
FD09 – Deuxième problème
R(s)=138
-12x=-60
x=\dfrac{-60}{-12}
x=5
| x | |
| f'(x) | |
| f(x) |
f(5)=162
FD08 – Premier problème
Pour faire connaitre ces produits, les dirigeants décident de créer une pochette « découverte » qui sera proposée au prix de 2 €.
On étudie la rentabilité de cette opération sur une journée sachant qu’au maximum 400 pochettes peuvent être fabriquées chaque jour.
a) 100 pochettes vendues par jour.
b) 400 pochettes vendues par jour.
a) 100 pochettes : 100 \times 2=200
b) 400 pochettes : 400 \times 2=800
Exprimer R(n) en fonction de n.
définie sur l’intervalle [0;400] telle que f(x)=-0,01x^2+5x+10.
donc -0,02x>-5
donc x<\dfrac{5}{0,02} ou x<250 soit I=[0;250[
FD07 – Premier exercice complet et problème
1) Calculer f'(x) où f' désigne la dérivée de la fonction f.
2) Étudier le signe de f'(x) sur l’intervalle I=[18;40].
3) Établir le tableau de variations de la fonction f sur l’intervalle I=[18;40].
4) En déduire la valeur de x pour laquelle la fonction f admet un maximum.
N(t)=-5t^3+225t^2-3240t+15250 Les heures sont dans l’intervalle I=[10;20]
1) Compléter le tableau de valeurs de la fonction N situé ci-dessous.
| t | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| N(t) | 350 | 400 | 450 |
2) Placer les points correspondants dans le repère situé ci-après. Tracer la courbe représentative de la fonction N sur l’intervalle I=[10;20].
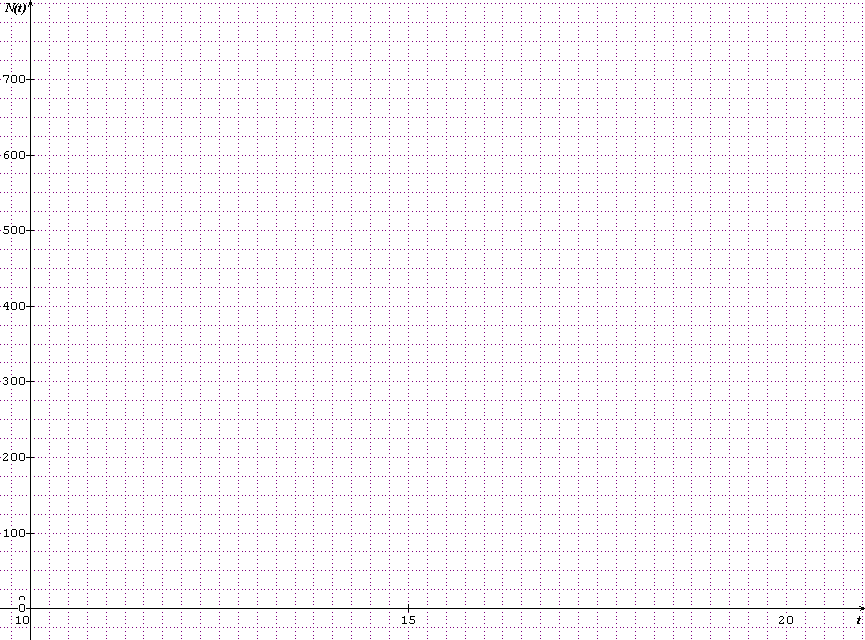
3) Déterminer graphiquement le nombre de clients présents à 15 heures 30 minutes. Laisser apparents les traits permettant la lecture graphique.
4) Soit N' la fonction dérivée de N. Déterminer N'(t).
5) Vérifier que N'(t)=0 équivaut à t^2-30t+216=0.
6) Résoudre cette équation.
7) Compléter le tableau de variation situé ci-dessous.
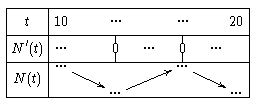
8) Déduire des résultats précédents l’heure à laquelle il faut prévoir un maximum de caissières pour fluidifier le passage aux caisses.
FD06 – Tableau de variation
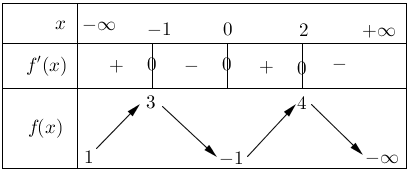
① Ce tableau se base sur l’ensemble de définition I de la fonction qui vous sera donné.
Dans ce tableau de variation doit figurer les abscisses de I ainsi que les valeurs particulières qui annulent la dérivée.
| x | -\infty | -1 | 0 | 2 | +\infty |
﹖⃝Ici l’ensemble de définition est ]-\infty;+\infty[ avec 3 valeurs particulières -1;0;2.
—————–
② On doit y trouver aussi une étude du signe de la dérivée.
| f'(x) | + | 0 | - | 0 | + |
﹖⃝Ici le signe de la dérivée change aux valeurs particulières -1;0;2.
—————–
③ Et enfin les variations de la fonction symbolisées par des flèches.
On en conclut les variations de la fonctions avec des flèches montantes pour de la croissance, descendante pour de la décroissance et horizontale pour la constance.
⚠ N’oubliez d’inscrire les valeurs des images des valeurs particulières par la fonction f.
① On calcule la dérivée de la fonction f : f'(x)=6x+12
② On résout l’équation f'(x)=0 : 6x+12=0 ou x=-2
La dérivée s’annule donc en -2, la fonction change de signe en ce point.
③ On étudie le signe de la dérivée de f :
f'(x)>0 quand x>-2
f'(x)<0 quand x<-2 On résume :
| f'(x) | - | 0 | + |
④ On calcule les valeurs des images des valeurs particulières.
f(-5)=3(-5)^2+12(-5)-5=10
f(-2)=3(-2)^2+12(-2)-5=-17
f(2)=3(2)^2+12(2)-5=31
⑤ On construit les flèches associées aux signes de la dérivées.
⑥ On obtient :
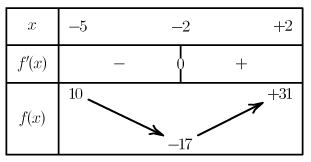
FD05 – Applications à l’étude des variations d’une fonction
Soit f une fonction dérivable sur un intervalle I :
Si f'(x)>0 alors la fonction est croissante sur I.
Si f'(x)=0 alors la fonction est constante sur I.
Si f'(x)<0 alors la fonction est décroissante sur I.
Si f(x)=2x alors f'(x)=2 or f'(x)>0 donc f est croissante.
Si f(x)=-3x alors f'(x)=-3 or f'(x)<0 donc f est décroissante.
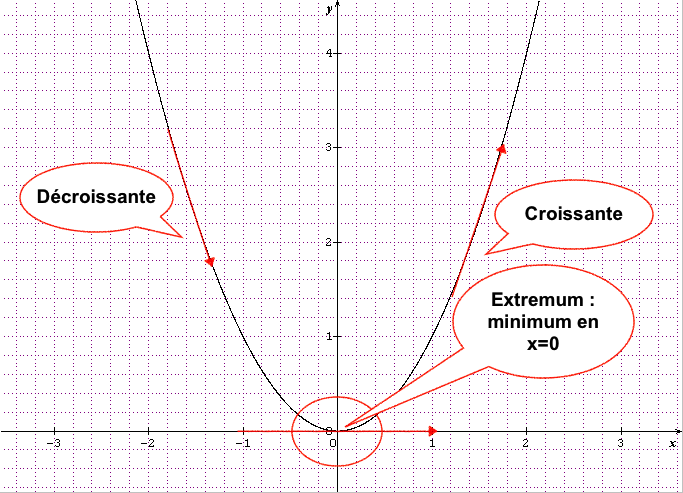
SI pour une valeur x_0 appartenant à l’intervalle I, f'(x_0) s’annule en changeant de signe alors la fonction f passe par un extremum (minimum ou maximum) pour x=x_0.
f'(x)=2x
Si x<0 alors f'(x)<0 donc la fonction est décroissante.
Si x=0 alors f'(x)=0 donc la fonction est constante.
Si x>0 alors f'(x)>0 donc la fonction est croissante.
La fonction f(x)=x^2 s’annule en x_0=0 en changeant de signe donc x_0=0 est un extremum ici un minimum.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
A l’aide du calcul de la dérivée, déterminer un extremum.
A l’aide du calcul de la dérivée, déterminer un extremum.
FD04 – QCM Dérivées
Cliquer sur le bouton « Départ » pour commencer le QCM
QCM Dérivées
Félicitation - vous avez complété QCM Dérivées.
Vous avez obtenu %%SCORE%% sur %%TOTAL%%.
Votre performance a été évaluée à %%RATING%%
FD03B – Exercices calcul de dérivées
f(x)=3x+2-\dfrac{2}{x}
f'(x)=3+\dfrac{2}{x^2} -> règle f+g
f(x)=-x^2+7x-10
f'(x)=-2x+7 -> règle f+g
f(x)=4x+8\sqrt{x}
f'(x)=4+\dfrac{4}{\sqrt{x}} -> règle f+g
FD-03A : Exercices calcul de dérivées
FD02 – Calcul de dérivées
Étant donnée une fonction f dérivable sur un intervalle I, la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction f en x est appelée fonction dérivée de la fonction f sur I et est notée f'.
I=\mathbb{R} représente l’ensemble des réels et I=\mathbb{R}^+ représente l’ensemble des réels positifs.
| Fonction | Expression | Fonction dérivée |
| Constante | a | 0 |
| Affine | ax+b | a |
| Carrée | x^2 | 2x |
| Cube | x^3 | 3x^2 |
| Inverse | \dfrac{1}{x} | -\dfrac{1}{x^2} |
| Racine carrée | \sqrt{x} | \dfrac{1}{2\sqrt{x}} |
Si f(x)=2x alors f'(x)=2 => Fonction linéaire
Si f(x)=2x+4 alors f'(x)=2 => Fonction affine (=fonction linéaire + fonction constante)
Si f(x)=x^2 alors f'(x)=2x => Fonction carrée
Si f(x)=x^3 alors f'(x)=3x^2 => Fonction cube
Si f(x)=\dfrac{1}{x} alors f'(x)=-\dfrac{1}{x^2} => Fonction inverse
Si f(x)=\sqrt{x} alors f'(x)=\dfrac{1}{2\sqrt{x}} => Fonction racine carrée
Étant donnée deux fonctions f et h dérivables sur un intervalle I et un réel k telles que h=k \times f et , la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction h en x est appelée fonction dérivée de la fonction h sur I et est notée h' et est égale à k \times f'.
On en déduit que h'(x)=k \times f'(x)=2 \times 1=2.
On en déduit que h'(x)=k \times f'(x)=3 \times 2x=6x.
On en déduit que h'(x)=k \times f'(x)=5 \times \dfrac{1}{2\sqrt{x}}=\dfrac{5}{2\sqrt{x}}.
Étant donnée trois fonctions f,g et h dérivables sur un intervalle I et telles que h=f+g, la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction h en x est appelée fonction dérivée de la fonction h sur I et est notée h' et est égale à f'+g'.
or f'(x)=2 et g'(x)=0. On en déduit que h'(x)=f'(x)+g'(x)=2+0=2.
or f'(x)=3x^2 et g'(x)=2x. On en déduit que h'(x)=f'(x)+g'(x)=3x^2+2x.
or f'(x)=\dfrac{1}{2\sqrt{x}} et g'(x)=2. On en déduit que h'(x)=f'(x)+g'(x)=\dfrac{1}{2\sqrt{x}}+2.
h(x)=2x^3-x^2+3x-2 donne h'(x)=6x^2-2x+3
FD01 : Approche de la dérivée
– à partir de son expression algébrique
f(x)=2x^3+2
– sa représentation graphique :
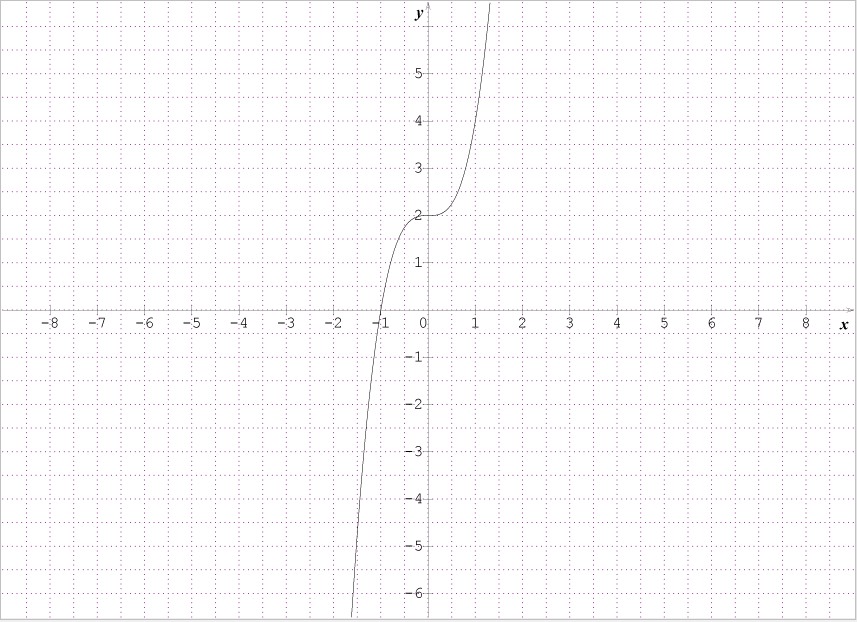
– et son tableau de valeurs :
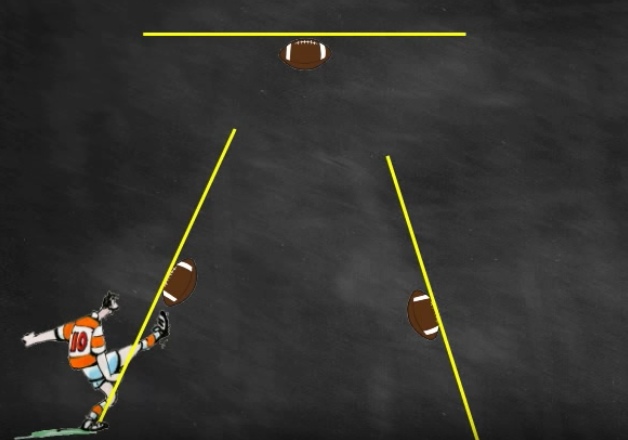
Prenons ce rugbyman qui tape dans un ballon :

Plusieurs trajectoires sont possibles :

La trajectoire peut être modélisée par une fonction numérique. Cette année, nous allons pouvoir prévoir les variations de la fonction numérique (ici la trajectoire).
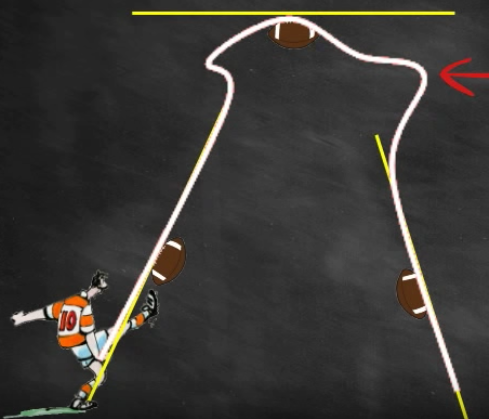
On va s’aider des tangentes en plusieurs points à la trajectoire du ballon.
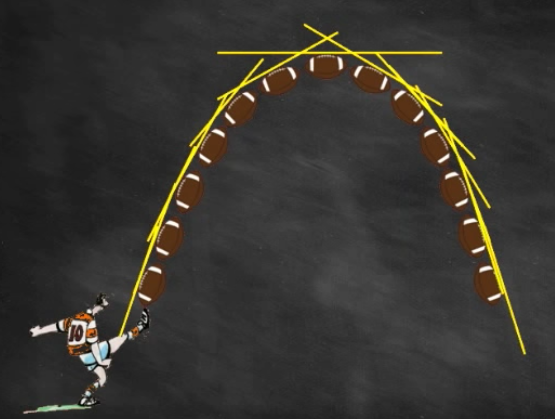
Pour être plus précis, on va multiplier les points de la trjectoire…

et calculer les tangentes.
On a donc réussi à affiner la trajectoire du ballon.
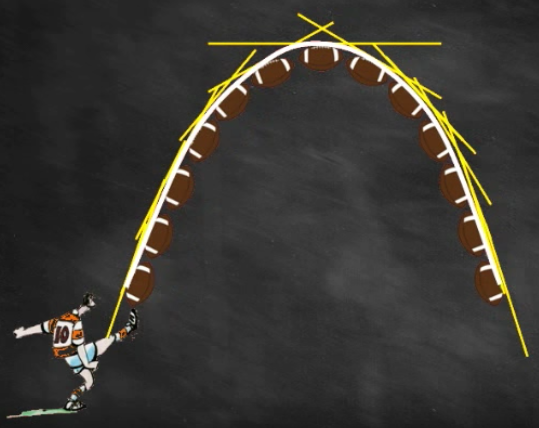
Les tangentes sont intéressantes car ce sont des droites donc faciles à étudier en mathématiques.
Les droites,représentations graphiques, ont été étudiées en seconde par leur fonction, la fonction affine f(x)=ax+b.
Une droite se caractérise avant tout par son coefficient directeur a qui nous indique si la droite est croissante ou décroissante.
Revenons une dernière fois sur notre rugbyman :
On voit que les tangentes ont un coefficient directeur positif quand la trajectoire monte et qu’elles ont un coefficient directeur négatif quand la trajectoire descend.
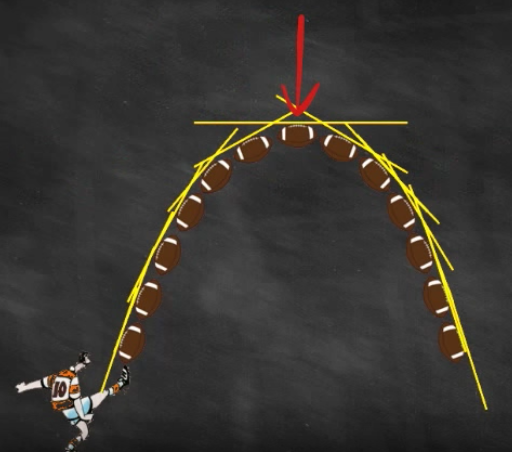
De plus lorsqu’on arrive au sommet de la trajectoire, le coefficient directeur de la tangente parallèle au sol (axe des abscisses) est nul.
– signe positif : trajectoire croissante
– signe nul : trajectoire constante
– signe négatif : trajectoire décroissante
C’est ce coefficient directeur de tangente que l’on appellera maintenant le nombre dérivé.
Il y autant de nombres dérivées que de tangentes possibles en chaque point de la courbe.
L’ensemble des nombres dérivés sont obtenus grâce à la fonction dérivée de la fonction numérique étudiée.
x \mapsto f'(x)
On dit « f prime de x ».
D02 – Cours
Notion de fonction dérivée
On appelle fonction dérivée de f (notée {f'}) la fonction qui associe, à toute valeur x de I, le nombre dérivé de f en x.
De la même façon que l’on définit une fonction continue sur un intervalle I, on définit une fonction dérivable sur un intervalle I. Pour certaines fonctions, la fonction dérivée n’existe pas en certains points. L’intervalle I permet de les enlever.
Pour mémoire, un intervalle s’écrit sous la forme \left [ 2,4 \right ] ou \left ] 2,+\infty \right[ .
Fonctions dérivées des fonctions de référence
| Si f(x)= | alors {f'}(x)= |
|---|---|
| ax+b | a |
| x^2 | 2x |
| x^3 | 3x^2 |
| \frac{1}{x} | \frac{-1}{x^2} |
| \sqrt{x} | \frac{1}{2 \sqrt{x}} |
| x^{a} | ax^{a-1} |
D01 – Approche par la tangente
| Points | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Coefficient directeur | 2 | 4 | 6 | -2 | -4 | -6 |
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| f‘(x) | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
| x | -3,5 | -2,5 | -2 | 0 | 2 | 4 | 8 | 25 |
|---|---|---|---|---|---|---|---|---|
| f‘(x) | -7 | -5 | -4 | 0 | 4 | 8 | 16 | 50 |
C’est à vous
\Box \quad {f'(x)}=2x \quad \Box \quad {f'(x)}=2x^2 \quad \Box \quad {f'(x)}=3x^2
Indice : Choisir les points d’abscisses -3,-2,-1,0,1,2,3 et trouver les ordonnées correspondantes f(-3),f(-2),f(-1),f(0),f(1),f(2),f(3)
Exemple : f(-3)=(-3)^3=(-3) \times (-3) \times (-3)=-27