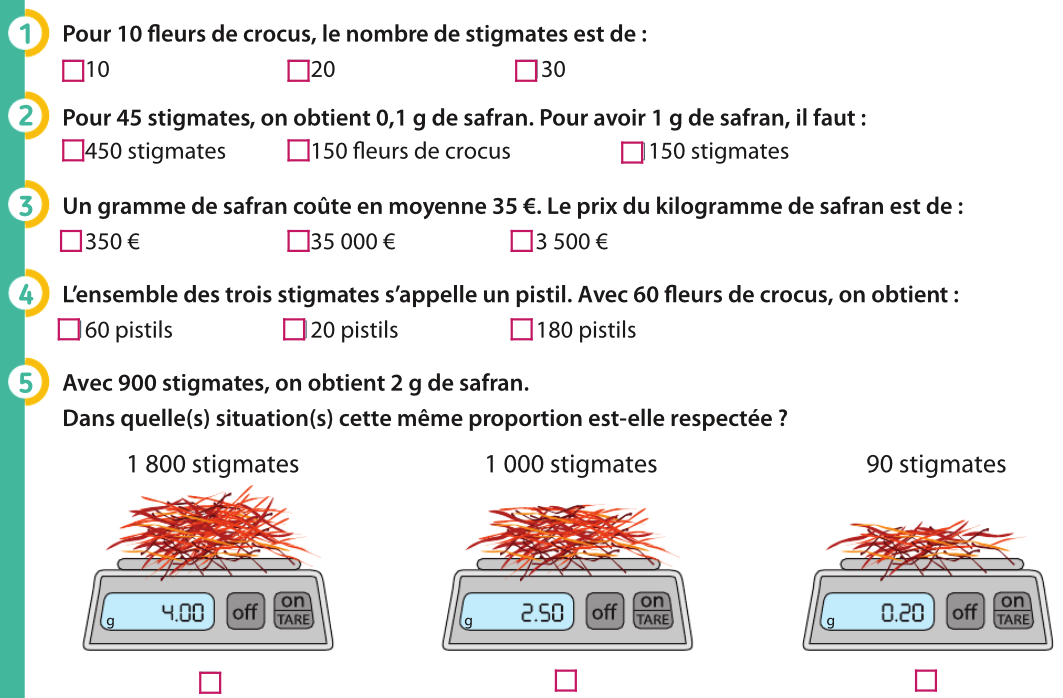
Correction Vidéo Exercice 2 TD12
Calcul littéral
Cliquer sur le bouton « Départ » pour commencer le QCM
Automatismes : Calcul littéral
Félicitation - vous avez complété Automatismes : Calcul littéral.
Vous avez obtenu %%SCORE%% sur %%TOTAL%%.
Votre performance a été évaluée à %%RATING%%
Reason : Premier pas
PRE-STA-02 : Indicateurs de dispersion : étendue, écart type, écart interquartile.
La température minimale est 9°C.
Attention c’est bien la différence entre les variables et non les effectifs.
L’étendue est ici de 13°C
Pour calculer le rang du premier quartile, on effectue le calcul suivant \dfrac{N \times1}{4} en arrondissant au chiffre supérieur.
Le troisième quartile Q_3 correspond à 75 % de l’effectif total.
Pour calculer le rang du troisième quartile, on effectue le calcul suivant \dfrac{N \times3}{4} en arrondissant au chiffre supérieur.
Ces paramètres sont liés à la médiane et indique la dispersion des valeurs autour de cette médiane.
\dfrac{31 \times1}{4}=7,75 Le premier quartile est au rang 8 soit 15°C.
\dfrac{31 \times3}{4}=23,25 Le troisième quartile est au rang 24 soit 18°C.
Q_3-Q_1
L’écart interquartile est de 3°C.
50% des températures sont différentes de 3°C.

Ce paramètre est lié à la moyenne et indique la dispersion des valeurs autour de cette moyenne.
L’écart-type est de 2,71°C.
PRE-STA-01 : Indicateurs de tendance centrale : mode, classe modale, moyenne, médiane.
Damien a relevé les températures du mois de mai à Paris sur un site internet. Les voici par jour :
| 14 | 19 | 17 | 18 | 20 | 19 | 22 |
| 21 | 17 | 14 | 18 | 16 | 17 | 16 |
| 16 | 14 | 17 | 15 | 16 | 12 | 12 |
| 16 | 13 | 9 | 16 | 17 | 19 | 15 |
| 16 | 16 | 17 |
\overline{x}=\dfrac{x_1+x_2+...+x_N}{N}
x est la variable statistique étudiée
N est l’effectif global
\overline{x}=16,2580645
On arrondit au centième en regardant le troisième chiffre après la virgule.
– S’il est inférieur ou égal à 4 soit (0,1,2,3,4) alors on arrondit au chiffre inférieur.
– S’il est supérieur ou égal à 5 soit (5,6,7,8,9) alors on arrondit au chiffre supérieur.
\overline{x}=16,26
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 1 | ||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 1 |
\overline{x}=\dfrac{x_1\times n_1+x_2\times n_2+...+x_N\times n_N}{N}
x est la variable statistique étudiée
n_1 est l’effectif de la variable x_1
N est l’effectif global et N=n_1+...+n_N
\overline{x}=16,2580645
Bien sûr nous allons trouvé la même moyenne.
Comment la calculer ?
1. Trier les valeurs dans l’ordre croissant
2. Déterminer l’effectif globale N
3.a. Si N est impair alors on trouve la médiane au rang \dfrac{N+1}{2}
3.b. Si N est pair alors on trouve la médiane entre le rang \dfrac{N}{2} et \dfrac{N+1}{2} donc on fait la demi-somme entre ses 2 valeurs.
La médiane se trouve au 16ème rang soit 16°C.
La médiane des températures est 16°C.
SEC-STA-03 – Regroupement par classes d’une série statistique
| 43 | 9 | 15 | 13 | 17 |
| 22 | 27 | 23 | 2 | 2 |
| 6 | 17 | 16 | 32 | 5 |
| 5 | 11 | 15 | 10 | 1 |
| 0 | 16 | 12 | 14 | 3 |
| Distance | Effectif | Fréquence | Degré |
|---|---|---|---|
| [0;10[ | |||
| [ | |||
| [ | |||
| [ | |||
| [ | |||
| Total |
Il est quantitatif discrte quand il est rangé sous forme de nombres distincts.
Il est quantitatif continu quand il est rangé sous forme de classes.
SEC-STA-02 : Extraire des informations d’une représentation d’une série statistique
SEC-STA-01 : Organiser des données statistiques en choisissant un mode de représentation adapté
CAP-PRO-04 : Utiliser et calculer des pourcentages
– 5€ offerts en bon d’achat tous les 50€ d’achat
– 6% de remise sous forme de bon d’achat sur tous vos achats
Elle pense que l’offre n°1 est plus intéressante pour elle, sachant qu’elle dépense 70€ en produits alimentaires.
A-t-elle raison ?
2. Compléter le tableau suivant
| Montant de l’achat | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Montant du bon d’achat | .. | .. | .. | .. | .. | .. | .. |
| Montant de l’achat | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Montant du bon d’achat | 0 | 5 | 5 | 5 | 5 | 5 | 10 |
| Prix initial | 70 | 100 |
| Economie | 5 | .. |
\dfrac{5 \times 100}{70}=7,42
| Prix initial | 70 | 100 |
| Economie | 5 | 7,42 |
Le nombre trouvé correspond au pourcentage de réduction, il est égale à 7,42 %.
5. Compléter le tableau suivant
| Montant de l’achat | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Montant du bon d’achat | .. | .. | .. | .. | .. | .. | .. |
| Montant de l’achat | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Montant du bon d’achat | 2,4 | 3 | 3,6 | 4,2 | 4,8 | 5,4 | 6 |
Avec l’offre 2 : Pour 70€, Camille reçoit un bon d’achat de 4,2€, soit 6% d’économie.
En effet l’offre 2 donne 6% d’économie contre 7,42% pour l’offre 1.
Appliquer un pourcentage à un nombre, c’est multiplier ce nombre par le pourcentage.
CAP-PRO-03 : Méthode pour tableau de proportionnalité
Par exemple, pour trouver la quantité de farine, le produit en croix donne 6 \times \dfrac{300}{4}=450
soit 450g de farine pour 6 oeufs.
CAP-PRO-02 : Des crêpes pour 20
a. Donner la valeur du coefficient de proportionnalité et compléter la deuxième ligne du tableau pour 40 crêpes.
| Farine (en g) | Oeufs | Lait (en cl) | Sucre (en cs) | Huile (en cs) | |
|---|---|---|---|---|---|
| 20 crêpes | 300 | 4 | 60 | 1 | 2 |
| 40 crêpes |
| Farine (en g) | Oeufs | Lait (en cl) | Sucre (en cs) | Huile (en cs) | |
|---|---|---|---|---|---|
| 20 crêpes | 300 | 4 | 60 | 1 | 2 |
| 40 crêpes | 600 | 8 | 120 | 2 | 4 |
| Farine (en g) | Oeufs | Lait (en cl) | Sucre (en cs) | Huile (en cs) | |
|---|---|---|---|---|---|
| 20 crêpes | 300 | 4 | 60 | 1 | 2 |
| ? crêpes | 6 |
Si vous bloquez, utilisez le lien vers la méthode
| Farine (en g) | Oeufs | Lait (en cl) | Sucre (en cs) | Huile (en cs) | |
|---|---|---|---|---|---|
| 20 crêpes | 300 | 4 | 60 | 1 | 2 |
| 30 crêpes | 450 | 6 | 90 | 1,5 | 3 |
Le coefficient de proportionnalité est ici de 1,5 pour passer de la première à la seconde ligne. On peut faire 30 crêpes avec 6 oeufs.
Le coefficient de proportionnalité est de 2.
| 1 crépe | 30 crepes | |
| Temps de cuisson en minutes | 2 | 60 |
Il peut faire 30 crêpes.
CAP-PRO-01 : Première situation
P02 : Principales instructions
Instruction conditionnelle
L’instruction si… alors introduit une condition.Si la condition est vérifiée, le traitement associé est effectué. L’instruction sinon peut compléter l’instruction « si…alors » pour exécuter un autre traitement lorsque la condition n’est pas vérifiée.
Louise doit appliquer une remise de 5 % sur les factures d’un montant supérieur à 500 €. Écrire un programme pour calculer le montant net à payer par le client à partir du montant de sa facture.
# si F est inférieur à 500 alors on stocke F dans N
N=F
else:
# si F est supérieur à 500 alors on stocke F*0,95 dans N
N=0,95*F
print(‘Le montant est ‘,N)
Créer un programme Python en suivant les instructions suivantes :
x ← nombre aléatoire entre 1 et 9.
y ← nombre aléatoire entre 1 et 9.
Afficher « x × y = »
Demander et saisir la valeur de z.
Si x × y = z alors afficher « Réponse exacte »
Sinon afficher « Réponse fausse, le résultat est (x × y) »
Instruction de boucle bornée
Une boucle bornée est utilisée pour répéter plusieurs fois la même suite d’instructions.En début de boucle, un compteur est initialisé à 1.Il augmente d’une unité à chaque traitement jusqu’au nombre n de répétitions demandées.
On utilise une boucle bornée pour simuler 10 lancers successifs d’un dé à 6 faces.
# si F est inférieur à 500 alors on stocke F dans N
x=randint(1,6)
Ecrire un programme Python permettant de simuler 20 lancers d’une pièce de monnaie et afficher le résultat de chaque lancer.Le nombre 0 est associé à PILE, le nombre 1 à FACE.
Que permet de faire le programme suivant:
for i in range(10):
#le carré d’un nombre s’écrit avec **2
y=-5x**2+10
print("x",x," ","f(x)=",y)
x=x+1
Instruction de boucle non bornée
Avec une boucle non bornée, la répétition de l’action dépend d’une condition.Tant que la condition est vraie, le traitement est répété. Si la condition est fausse, la boucle est arrêtée.
On utilise une boucle non bornée pour savoir dans combien de temps Soraya pourra acheter un smartphone qui coûte 190 €. Actuellement, elle possède 32 € dans sa tirelire et elle a décidé d’économiser chaque semaine 8 € sur son argent de poche.
S=32
n=0
while S<190:
n=n+1
S=S+8
print(‘nombre de semaines’,n)
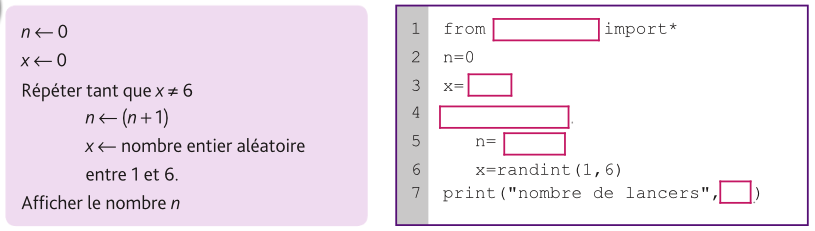
Pour commencer une partie de dés, Malik doit obtenir un six avec un dé.Pour connaître, en moyenne, combien de lancers du dé sont nécessaires pour obtenir six, il a commencé à écrire l’algorithme et le programme ci-dessous.
Fonctions sans paramètre
Une fonction est un sous-programme qui réalise un traitement avec les arguments nécessaires et qui rend une valeur.Une fonction n’affiche pas de réponse à l’écran, elle doit être intégrée à un programme.
On utilise les fonctions quand on veut réutiliser celle-ci plusieurs fois dans le programme. Elle permet de clarifier aussi la programmation quand plusieurs fonctions existent. Cette fonction sans paramètre est définie en premier et est appelée ensuite dans le programme. Elle permet d’afficher un compteur 0,1,2,3
i = 0
while i < 3:
print(i)
i=i+1
print("bonjour")
compteur3()
Créer un programme qui définie une fonction simulant le tirage d'un dé à 20 faces. Effectuer ensuite 2 lancers de celui-ci.
Fonctions avec paramètres
Une fonction est un sous-programme qui réalise un traitement avec les arguments nécessaires et qui rend une valeur.Une fonction n’affiche pas de réponse à l’écran, elle doit être intégrée à un programme.
Les fonctions avec paramètres permettent de prendre un ou plusieurs paramètres définies au travers la fonction mais aussi variable à souhait. Ici la fonction a comme paramètre la variable 'stop' permettant de varier la taille du décompte.
i = 0
while i < stop:
print(i)
i=i+1
compteur(4)
compteur(2)
Corriger le programme suivant pour qu'il affiche le décompte 1,2,3,4,5,6,7,8
i = 0
while i < stoppe:
print(i)
i=i-1
a = 5
compteur(a)
P01 : Premier programme Python
Dans cette partie, nous allons utiliser le module Idle de Python.
Il est possible d’utiliser la ligne de commande pour des programmes très courts mais l’Idle est préférable pour les programmes plus longs et surtout garde une trace de l’activité de l’élève.
Préalable à l’utilisation des mathématiques en programmation Python
Comment le faire ?
Commentaires en Python
Les commentaires sous Python se font avec un dièse « # » en début de ligne
Comment le faire ?
from maths import *
# Fin de l’importation
Instructions d’entrée et de sortie
L’interaction avec l’utilisateur en entrée s’effectuera avec l’instruction d’entrée « input » et l’affichage de la réponse à l’écran avec l’instruction de sortie « print »
from maths import *
# Variable R demandée à l’utilisateur à l’aide de l’instruction input
R=input(‘Rayon’)
Qu’est ce qu’un typage ?
A=3 par exemple stocke le ‘nombre entier’ dans la variable A
Message=’C’est faux’ par exemple stocke la chaîne de caractère ‘C’est faux’ dans la variable Message.
Les trois types principaux a utilisé sont int pour un nombre entier, float pour un nombre décimal et str pour une chaîne de caractère.
Stockage dans une variable
périmètre du cercle ne fonctionne pas mais perimetre_du_cercle lui fonctionnera.
# Ici nous allons stocker dans A l’aire d’un disque connaissant le rayon
A=pi*R*2
Affichage du résultat en sortie
# Pour parfaire l’affichage, on ajoute du texte avant la valeur de la variable séparé par une virgule qui sera concaténé (ajouter du texte à un autre).
print(‘Aire : ‘,A)
Premier programme de la calcul d’une aire A d’un disque connaissant le rayon R
R=input(‘Rayon’)
A=pi*R*2
print(‘Aire : ‘,A)
TERFD11 – Problème type CCF
FD10 – Troisième problème
Le coût de production C(n) exprimé en milliers d’euro pour n articles est donné par la fonction C avec : C(n)=0,02n^2-2n+98 pour n appartenant à l’intervalle [50 ; 150].
Le montant des ventes V(n) exprimé en milliers d’euro est pour sa part donné par la fonction V avec V(n)=1,5n pour n appartenant à l’intervalle [50 ; 150].
| n | 50 | 60 | 75 | 90 | 100 | 125 | 150 |
| C(n) | … | 50 | … | … | 98 | … | 248 |
C(75)=60,5
C(90)=80
C(125)=160,5
Exprimer B(n) en fonction de n et déterminer la dérivée B'(n).
B(n)==1,5n-(0,02n^2-2n+98)
B(n)=-0,02n^2+3,5n-98
B'(n)=-0,04n+3,5
-0,04n+3,5=0
-0,04n=-3,5
n=87,5
Le nombre d’article est maximum pour n=87,5 car la fonction B est une fonction carrée et sa dérivée change de signe en n=87,5.
FD09 – Deuxième problème
R(s)=138
-12x=-60
x=\dfrac{-60}{-12}
x=5
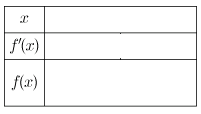
| x | |
| f'(x) | |
| f(x) |
f(5)=162
FD08 – Premier problème
Pour faire connaitre ces produits, les dirigeants décident de créer une pochette « découverte » qui sera proposée au prix de 2 €.
On étudie la rentabilité de cette opération sur une journée sachant qu’au maximum 400 pochettes peuvent être fabriquées chaque jour.
a) 100 pochettes vendues par jour.
b) 400 pochettes vendues par jour.
a) 100 pochettes : 100 \times 2=200
b) 400 pochettes : 400 \times 2=800
Exprimer R(n) en fonction de n.
définie sur l’intervalle [0;400] telle que f(x)=-0,01x^2+5x+10.
donc -0,02x>-5
donc x<\dfrac{5}{0,02} ou x<250 soit I=[0;250[
FD07 – Premier exercice complet et problème
1) Calculer f'(x) où f' désigne la dérivée de la fonction f.
2) Étudier le signe de f'(x) sur l’intervalle I=[18;40].
3) Établir le tableau de variations de la fonction f sur l’intervalle I=[18;40].
4) En déduire la valeur de x pour laquelle la fonction f admet un maximum.
N(t)=-5t^3+225t^2-3240t+15250 Les heures sont dans l’intervalle I=[10;20]
1) Compléter le tableau de valeurs de la fonction N situé ci-dessous.
| t | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| N(t) | 350 | 400 | 450 |
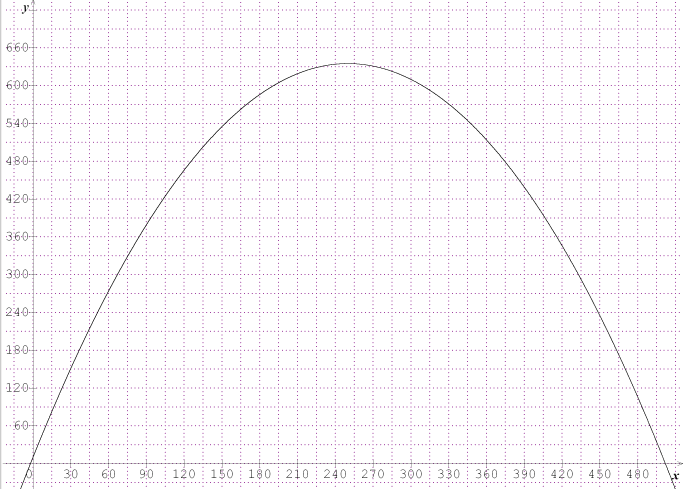
2) Placer les points correspondants dans le repère situé ci-après. Tracer la courbe représentative de la fonction N sur l’intervalle I=[10;20].
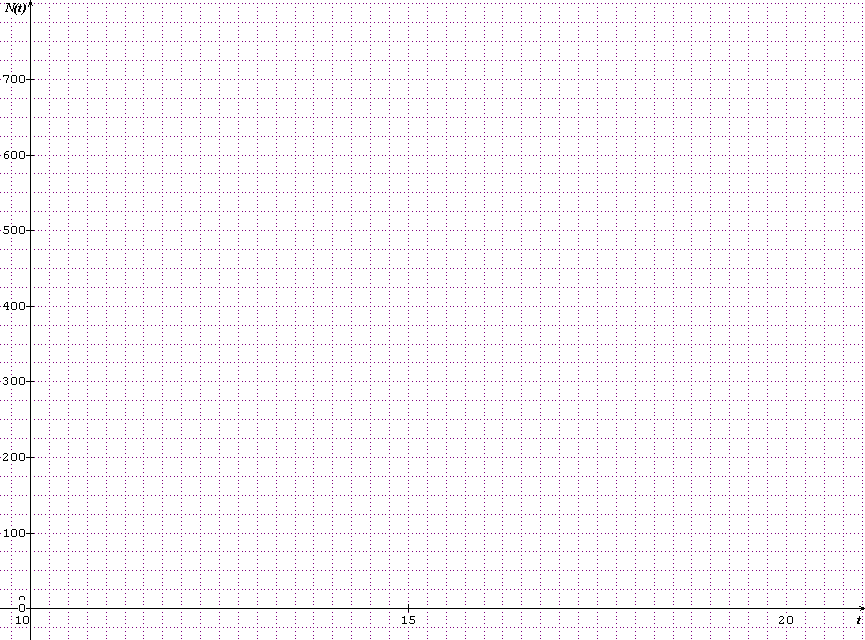
3) Déterminer graphiquement le nombre de clients présents à 15 heures 30 minutes. Laisser apparents les traits permettant la lecture graphique.
4) Soit N' la fonction dérivée de N. Déterminer N'(t).
5) Vérifier que N'(t)=0 équivaut à t^2-30t+216=0.
6) Résoudre cette équation.
7) Compléter le tableau de variation situé ci-dessous.
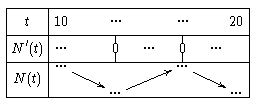
8) Déduire des résultats précédents l’heure à laquelle il faut prévoir un maximum de caissières pour fluidifier le passage aux caisses.