Signe de la dérivée et variations
Soit f une fonction dérivable sur un intervalle I :

Si f'(x)>0 alors la fonction est croissante sur I.
Si f'(x)=0 alors la fonction est constante sur I.
Si f'(x)<0 alors la fonction est décroissante sur I.

Soit f une fonction dérivable sur un intervalle I.
Si f(x)=2x alors f'(x)=2 or f'(x)>0 donc f est croissante.

Soit f une fonction dérivable sur un intervalle I.
Si f(x)=-3x alors f'(x)=-3 or f'(x)<0 donc f est décroissante.

Recherche d’extremum
SI pour une valeur x_0 appartenant à l’intervalle I, f'(x_0) s’annule en changeant de signe alors la fonction f passe par un extremum (minimum ou maximum) pour x=x_0.

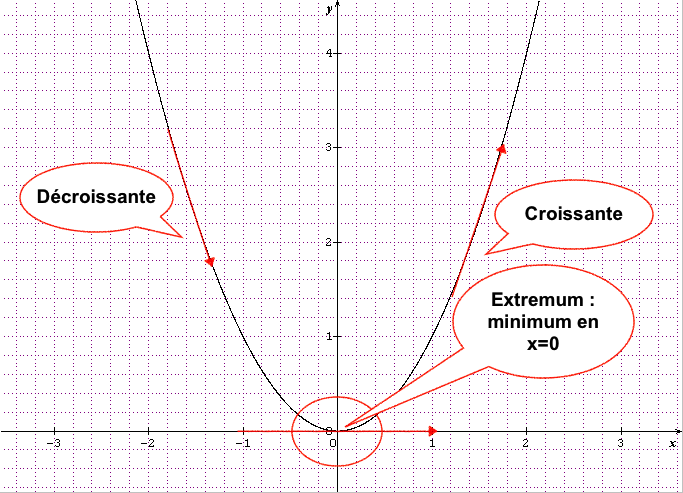
Soit f une fonction dérivable sur un intervalle I telle que f(x)=x^2.
f'(x)=2x
Si x<0 alors f'(x)<0 donc la fonction est décroissante.
Si x=0 alors f'(x)=0 donc la fonction est constante.
Si x>0 alors f'(x)>0 donc la fonction est croissante.
La fonction f(x)=x^2 s’annule en x_0=0 en changeant de signe donc x_0=0 est un extremum ici un minimum.

1.Soit f une fonction dérivable sur un intervalle I=[-2;2] telle que f(x)=-3x^2.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.

2.Soit f une fonction dérivable sur un intervalle \mathbb{R} telle que f(x)=-4x^3.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.

3.Soit f une fonction dérivable sur un intervalle \mathbb{R^+*} telle que f(x)=-\sqrt{x}.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.

4.Soit f une fonction dérivable sur un intervalle I=[1;7] telle que f(x)=\dfrac{-3}{x}.
A l’aide du calcul de la dérivée, déterminer un extremum.

5.Soit f une fonction dérivable sur un intervalle I=[-1;3] telle que f(x)=x^2-2x+1.
A l’aide du calcul de la dérivée, déterminer un extremum.