Proba7 : Exercice d’arbre
Une urne contient trois boules de couleurs différentes (jaune, verte, bleue). On tire au hasard une première boule, on la remet dans l’urne après avoir noté sa couleur. On tire une seconde boule, on note sa couleur.
1.Construire l’arbre correspondant à cette expérience aléatoire
2.A l’aide d’un arbre déterminer toutes les issues de cette expérience aléatoire.
Il y a 9 issues pour cette expérience.
Ω={JJ,JV,JB,VJ,VV,VB,BJ,BV,BB}.
Ω={JJ,JV,JB,VJ,VV,VB,BJ,BV,BB}.
3.Déterminer les issues de l’événement « les deux boules sont de la même couleur ».
Les issues sont : JJ,VV,BB
4.Quelle est la probabilité de tirer deux boules de même couleur ?
P=3/9=1/3
5.Quelle la probabilité de tirer deux boules bleues ?
P=1/9
6.Quelle est la probabilité de tirer deux boules dont la première est verte ?
P=3/9=1/3
D02 – Cours
Notion de fonction dérivée
On définit une fonction f dérivable sur un intervalle I.
On appelle fonction dérivée de f (notée {f'}) la fonction qui associe, à toute valeur x de I, le nombre dérivé de f en x.
On appelle fonction dérivée de f (notée {f'}) la fonction qui associe, à toute valeur x de I, le nombre dérivé de f en x.
De la même façon que l’on définit une fonction continue sur un intervalle I, on définit une fonction dérivable sur un intervalle I. Pour certaines fonctions, la fonction dérivée n’existe pas en certains points. L’intervalle I permet de les enlever.
Pour mémoire, un intervalle s’écrit sous la forme \left [ 2,4 \right ] ou \left ] 2,+\infty \right[ .
Fonctions dérivées des fonctions de référence
| Si f(x)= | alors {f'}(x)= |
|---|---|
| ax+b | a |
| x^2 | 2x |
| x^3 | 3x^2 |
| \frac{1}{x} | \frac{-1}{x^2} |
| \sqrt{x} | \frac{1}{2 \sqrt{x}} |
| x^{a} | ax^{a-1} |
D01 – Approche par la tangente
Ouvrir Géogébra
Dans la zone de saisie, entrer f(x)=x^2
1.Quelle est la fonction saisie ?
C’est la fonction carrée.
2.Quelles sont ses caractéristiques graphiques ?
La fonction est symétrique par rapport à x=0. Elle est donc décroissante jusqu’à 0 puis croissante après 0.
Dans la zone de saisie, entrer les points (1,1) (2,4) (3,9) (-1,1) (-2,4) (-3,9)
3.Les points appartiennent-ils à la courbe ?
f(1)=1 f(2)=4 f(3)=9 et par symétrie f(-1)=1 f(-2)=4 f(-3)=9
En appuyant sur le 4ème bouton, choisir « Tangentes » pour connaître l’équation de la tangente d’une courbe en un point. Déterminer les équations des tangentes des différents points A,B,C puis D,E,F.
Procédure : Pour chaque point, il faut cliquer sur ce point et la courbe. Des équations de type affine y=ax+b vont apparaître dans la zone de saisie…Pour mémoire : a est le coefficient directeur d’une équation affine.
4.Compléter le tableau suivant :
| Points | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Coefficient directeur | 2 | 4 | 6 | -2 | -4 | -6 |
On note {f'(x)} le coefficient directeur de la tangente à la courbe représentative C au point d’abscisse x.
5.Compléter le tableau suivant :
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| f‘(x) | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
6. A l’aide des résultats du tableau remplissez en conjecturant le tableau suivant :
| x | -3,5 | -2,5 | -2 | 0 | 2 | 4 | 8 | 25 |
|---|---|---|---|---|---|---|---|---|
| f‘(x) | -7 | -5 | -4 | 0 | 4 | 8 | 16 | 50 |
7. Plus généralement, pour tout nombre x, conjecturer la formule donnant {f'(x)} en fonction de x :
\Box \quad {f'(x)}=2+x \quad \Box \quad {f'(x)}=2x \quad \Box \quad {f'(x)}=x^2
La formule qui paraît logique au vue des résultats obtenus est : {f'(x)}=2x
La fonction x \mapsto 2x est la dérivée de la fonction f(x), notée {f'(x)}.
C’est à vous
Avec la même procédure, trouver la dérivée de la fonction f(x)=x^3.
\Box \quad {f'(x)}=2x \quad \Box \quad {f'(x)}=2x^2 \quad \Box \quad {f'(x)}=3x^2
Indice : Choisir les points d’abscisses -3,-2,-1,0,1,2,3 et trouver les ordonnées correspondantes f(-3),f(-2),f(-1),f(0),f(1),f(2),f(3)
Exemple : f(-3)=(-3)^3=(-3) \times (-3) \times (-3)=-27
\Box \quad {f'(x)}=2x \quad \Box \quad {f'(x)}=2x^2 \quad \Box \quad {f'(x)}=3x^2
Indice : Choisir les points d’abscisses -3,-2,-1,0,1,2,3 et trouver les ordonnées correspondantes f(-3),f(-2),f(-1),f(0),f(1),f(2),f(3)
Exemple : f(-3)=(-3)^3=(-3) \times (-3) \times (-3)=-27
La fonction f(x)=x^3 a pour dérivée la fonction {f'(x)}=3x^2.
Not.Fonc.01
Croissance décroissance
Une fonction f est croissante sur un intervalle I si f(x) augmente lorsque x augmente.
Si : x_1<x_2[/latex] alors : [latex]f(x_1)<f(x_2)[/latex] Une fonction [latex]f[/latex] est décroissante sur un intervalle I si [latex]f(x)[/latex] diminue lorsque [latex]x[/latex] augmente. Si : [latex]x_1<x_2[/latex] alors : [latex]f(x_1)>f(x_2)
Si : x_1<x_2[/latex] alors : [latex]f(x_1)<f(x_2)[/latex] Une fonction [latex]f[/latex] est décroissante sur un intervalle I si [latex]f(x)[/latex] diminue lorsque [latex]x[/latex] augmente. Si : [latex]x_1<x_2[/latex] alors : [latex]f(x_1)>f(x_2)
SG13 : Problème avec des suites
Augmentation
Un patron propose à ses employés deux modes d’augmentation de leur salaire mensuel.
Un patron propose à ses employés deux modes d’augmentation de leur salaire mensuel.
Option A : une augmentation fixe du salaire mensuel de 50 € au premier janvier de chaque année.
Marie est embauchée dans l’entreprise avec un salaire de 1 500 € par mois. Elle choisit d’être augmentée suivant l’option A. On note M_n son salaire après n années passées dans l’entreprise. On a M_0 = 1500 .
a) Calculer M_1 et M_2 .
b) Exprimer M_{n+1} en fonction de M_n . En déduire la nature de la suite ( M_n ).
c) Exprimer M_n en fonction de n.
d) Calculer M_{20} .
e) A partir de combien d’années son salaire mensuel sera-t-il d’au moins 1 800 € ?
Option B : une augmentation de 3 % du salaire mensuel de l’année précé- dente au premier janvier de chaque année.
Jean est embauché la même année que Marie avec un salaire de 1 500 € par mois. Il choisit d’être augmenté suivant l’option B. On note J_n son salaire après n années passées dans l’entreprise. On a J_0 = 1500 .
a) Calculer J_1 et J_2 .
b) Exprimer J_{n+1} en fonction de J_n . En déduire la nature de la suite ( J_n ).
c) Exprimer J_n en fonction de n.
d) Calculer J_{20} . (Arrondir au centime près).
e) A l’aide de la calculatrice, déterminer à partir de combien d’années son salaire mensuel sera d’au moins 1 800 € ?
A partir de combien d’années passées dans l’entreprise, le salaire mensuel de Jean sera-t-il supérieur à celui de Marie ?
Proba1 – Vocabulaire des probabilités
Définition
Une expérience aléatoire est une expérience dont on peut déterminer toutes les issues possibles mais sans savoir laquelle va se réaliser.
Exemple :
Dans un jeu de 32 cartes, l’expérience « tirer une carte au hasard sans tenir compte de sa couleur » est une expérience aléatoire car :
– on peut déterminer toutes les issues possibles : ici on peut obtenir un 7, un 8 , un 9, un 10, un valet, une dame, un roi ou un as.
– on ne sait pas laquelle de ces issues va se réaliser.
– on peut déterminer toutes les issues possibles : ici on peut obtenir un 7, un 8 , un 9, un 10, un valet, une dame, un roi ou un as.
– on ne sait pas laquelle de ces issues va se réaliser.
Définition
L’univers Ω (lire oméga) d’une expérience aléatoire est l’ensemble de tous les résultats possibles. Un événement est le résultat d’une expérience aléatoire : c’est une partie de l’univers.
Exemples :
Dans un jeu de 32 cartes, l’expérience « tirer une carte au hasard sans tenir compte de sa couleur », a pour univers l’ensemble des issues suivantes : Ω = {7; 8; 9; 10; valet; dame; roi; as}.
L’évènement A « on gagne si on tire une figure », est une partie de l’univers. Les issues possibles sont : A = {valet; dame; roi}.
Propriétés
Proba2. Calculer une probabilité
Enoncé
Ali et Laura jouent avec un jeu de 32 cartes avec la règle suivante : chaque joueur tire une carte ; il gagne si c’est une figure. Ali joue en premier. Il se demande combien il a de chances de gagner.
1. Quel est l’univers Ω (les issues possibles) de ce tirage ?
Ω ={7; 8; 9; 10; valet; dame; roi; as}
2. Quelles sont les issues possible de l’évènement A « je tire une figure » ?
A ={valet; dame; roi; as}
Définition
Pour calculer la probabilité d’un évènement, on divise le nombre d’issues favorables par le nombre d’issues possibles. p(A)=\dfrac{\text{nb d'issues favorables}}{\text{nb total d'issues possibles}}
3. Quelle est la probabilité p(A) de l’évènement A?
On a 3 issues favorables pour 8 issues possibles au total
p(A)=\dfrac{3}{8}= 0,375
p(A)=\dfrac{3}{8}= 0,375
Définition
L’évènement contraire de A est noté \overline{A}. Il comporte les issues qui n’entrent pas dans A.
Exemple :
\overline{A} = {7; 8; 9; 10; as}
4. Quelle est la probabilité p(\overline{A}) de l’évènement \overline{A}?
On a 5 issues favorables pour 8 issues possibles au total
p(\overline{A})=\dfrac{5}{8}= 0,625
p(\overline{A})=\dfrac{5}{8}= 0,625
5. Quelle relation permet de déterminer la probabilité p(\overline{A}) de l’évènement \overline{A} à l’aide de la probabilité de l’évènement A ?
p(\overline{A})= 1 – p(A) = 1 – 0,375 = 0,625
Proba3. Probabilité d’un évènement et fréquences des échantillons
Définition
Le résultat d’une expérience aléatoire est dû au hasard, la fréquence de chaque échantillon est donc aléatoire. Mais plus le nombre d’échantillons est grand, plus la moyenne des fréquences des échantillons est proche de la probabilité de l’événement.
Exemple :
D’après Météo France, il pleut 128 jours par an sur la ville. Pour vérifier si l’apparition de la pluie est due au hasard on va simuler la prévision de la pluie sur différentes périodes.
A. SIMULATION
1. Quelle est la probabilité p(A) de l’évènement A « Avoir un jour de pluie »?
Il y a 128 jours favorables sur 365 jours possibles
p(A)=\dfrac{128}{365}= 0,35
p(A)=\dfrac{128}{365}= 0,35
2. Simulation sur une année.
Ouvrir une feuille de calcul d’excel.
Dans la colonne A, saisir les jours de 1 à 365.
Dans la colonne B, afficher 1 pour un jour de pluie et 0 pour un jour sans pluie. Quelle est la formule permettant de faire la simulation d’un jour de pluie ?
Dans la colonne A, saisir les jours de 1 à 365.
Dans la colonne B, afficher 1 pour un jour de pluie et 0 pour un jour sans pluie. Quelle est la formule permettant de faire la simulation d’un jour de pluie ?
=ENT(ALEA()+0.35)
Saisir cette formule dans la cellule B1, puis copier-la jusqu’à la cellule B365.
Dans la colonne C, afficher le cumul des nombres de jours de pluie :
C1:=B1 ; C2:=C1+B2 ; puis copier C2 jusqu’en C365.
Dans la colonne D, afficher la fréquence des jours de pluie :
D1:=C1/A1, puis recopier jusqu’en D365
Sélectionner la colonne D puis insérer un graphique de forme « nuage de points ». Appuyer F9 pour réaliser plusieurs simulations.
Le nuages de points obtenu ressemble à celui-ci.
Dans la colonne C, afficher le cumul des nombres de jours de pluie :
C1:=B1 ; C2:=C1+B2 ; puis copier C2 jusqu’en C365.
Dans la colonne D, afficher la fréquence des jours de pluie :
D1:=C1/A1, puis recopier jusqu’en D365
Sélectionner la colonne D puis insérer un graphique de forme « nuage de points ». Appuyer F9 pour réaliser plusieurs simulations.
Le nuages de points obtenu ressemble à celui-ci.
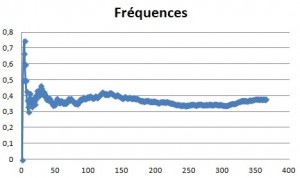
B. INTERPRETATIONS
1. Noter dans le tableau suivant la moyenne des fréquence des jours de pluie obtenus par simulation.
| Durées | Semaine (7 jours) | Quinzaine (15 jours) | Mois (30 jours) | Trimestre (90 jours) | Semestre (180 jours) | Année (365 jours) |
| Fréquence (selon simulation) | …….. | …….. | …….. | …….. | …….. | …….. |
Les résultats dépendent de vos simulations, voici un exemple :
| Fréquence | 0,43 | 0,36 | 0,40 | 0,39 | 0,37 | 0,35 |
2. Expliquer comment évolue la moyenne des fréquences lorsque le nombre de jours de l’échantillon augmente.
La fréquence est très variable quand le nombre de jours est petit, mais plus le nombre de jours augmente plus la moyenne des fréquences se stabilise et se rapproche de p=0,35.
Proba4. Probabilités lors de choix successifs
Définition
Lors d’un choix successif dans un ensemble de n éléments, il y a :
– n possibilités pour le 1er choix,
– (n – 1) possibilités pour le 2nd choix,
– (n – 2) possibilités pour le 3e, etc.
– n possibilités pour le 1er choix,
– (n – 1) possibilités pour le 2nd choix,
– (n – 2) possibilités pour le 3e, etc.
Exemple :
Prenons un jeu de 32 cartes, tirons successivement 2 cartes sans remise.
Soit A l’évènement « obtenir deux couleurs différentes ».
Soit A l’évènement « obtenir deux couleurs différentes ».
1. Calculer la probabilité de A lors du premier tirage
Nb d’issues favorables : 4
Nb d’issues possibles : 32
p(A)=\dfrac{4}{32}= 0,125
Nb d’issues possibles : 32
p(A)=\dfrac{4}{32}= 0,125
2. Calculer la probabilité de A lors du deuxième tirage
Nb d’issues favorables : 3
Nb d’issues possibles : 31
p(A)=\dfrac{3}{31}= 0,097
Nb d’issues possibles : 31
p(A)=\dfrac{3}{31}= 0,097
Proba5. Simuler un tirage avec un arbre des évènements
Définition
Un arbre des évènements est un schéma permettant de déterminer toutes les issues possibles lors d’une succession d’expériences aléatoires.
A chaque étape il faut notifier une issue possible par une ramification.
La somme des probabilités de chaque étape est égale à 1.
A chaque étape il faut notifier une issue possible par une ramification.
La somme des probabilités de chaque étape est égale à 1.
Exemple
Une urne contient 2 boules rouges et 1 boule Verte.
On réalise deux tirages successifs avec remise.
Voici l’arbre des évènements représentant cette expérience.
On réalise deux tirages successifs avec remise.
Voici l’arbre des évènements représentant cette expérience.
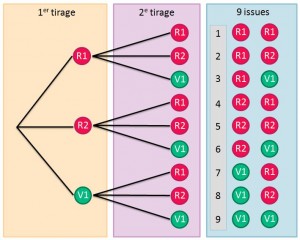
Application
Une urne contient 2 boules rouges, 3 boules Bleues et 4 boules Vertes.
On réalise trois tirages successifs sans remise.
On réalise trois tirages successifs sans remise.
1. Combien de possibilités avons-nous au premier tirage ?
Au premier tirage on a 3 possibilités correspondant à chacune des couleurs Rouge, Bleu et Vert.
2. Combien de possibilités avons-nous au deuxième tirage ?
Au deuxième tirage il existe encore des boules de chacune des trois couleurs, on a 3 possibilités correspondant à chacune des couleurs Rouge, Bleu et Vert.
3. Combien de possibilités avons-nous au troisième tirage ?
Si une boule rouge a été tirée à chaque fois des deux premiers tirages, il n’y a plus de boules rouges dans l’urne. Donc ce cas il ne reste plus que deux possibilités : bleu et Vert.
Sinon il reste toujours 3 possibilités car il existe encore des boules des trois couleurs.
Sinon il reste toujours 3 possibilités car il existe encore des boules des trois couleurs.
4. Réaliser un arbre des évènements correspondant à cette expérience.
5. Combien existe-t-il d’issues possibles au total ?
On a 26 issues possibles.
Soit l’évènement A « Obtenir trois boules de couleurs différentes ».
6. Combien existe-t-il d’issues favorables à l’évènement A ?
On a 6 issues favorables.
7. Quelle est la probabilité de l’évènement A ?
p(A)=\dfrac{6}{26}= 0,231
Soit l’évènement B « Obtenir au moins deux boules de couleurs identiques ».
8. Combien existe-t-il d’issues favorables à l’évènement B ?
On a 20 issues favorables.
9. Quelle est la probabilité de l’évènement B ?
p(A)=\dfrac{20}{26}= 0,769
Proba6. Opérations sur les probabilités
Définition
A et B sont deux événements d’une expérience aléatoire.
=> L’intersection des événements, notée A ∩ B, est l’ensemble des résultats qui réalisent à la fois les deux événements A et B.
=> La réunion des événements, notée A ∪ B, est l’ensemble des résultats qui réalisent l’un ou l’autre des événements A et B.
=> La probabilité de la réunion des événements A et B se calcule par la relation :
p(A∪B) = p(A) + p(B) – p(A∩B).
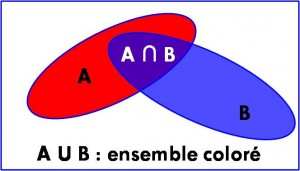
=> L’intersection des événements, notée A ∩ B, est l’ensemble des résultats qui réalisent à la fois les deux événements A et B.
=> La réunion des événements, notée A ∪ B, est l’ensemble des résultats qui réalisent l’un ou l’autre des événements A et B.
=> La probabilité de la réunion des événements A et B se calcule par la relation :
p(A∪B) = p(A) + p(B) – p(A∩B).
Exemple :
La classe de terminale GA participe à la journée sportive de solidarité Bouge Ton Coeur. On interroge les élèves sur leur participation :
Sur 20 filles 12 participent dans une équipe, sur 10 garçons il n’y a que 40% qui participent ans un équipe.
Sur 20 filles 12 participent dans une équipe, sur 10 garçons il n’y a que 40% qui participent ans un équipe.
1. Compléter le tableau suivant :
| Elèves | Joueurs | Spectateurs | TOTAL |
| Garçons | …….. | …….. | …….. |
| Filles | …….. | …….. | …….. |
| TOTAL | …….. | …….. | …….. |
| Elèves | Joueurs | Spectateurs | TOTAL |
| Garçons | 4 | 6 | 10 |
| Filles | 12 | 8 | 20 |
| TOTAL | 16 | 14 | 30 |
2. Calculer la probabilité de l’évènement A « l’élève interrogé est une fille ».
p(A)=\dfrac{20}{30}= 0,67
3. Calculer la probabilité de l’évènement B « l’élève interrogé est un joueur ».
p(B)=\dfrac{16}{30}= 0,53
4. Cocher la bonne notation de l’évènement C « l’élève interrogé est une fille joueuse dans une équipe ».
\quad \Box A U B \quad \Box A ∩ B \quad \Box A x B
\quad \Box A U B \quad \Box A ∩ B \quad \Box A x B
\quad \Box A U B \quad \boxtimes A ∩ B \quad \Box A x B
5. Calculer la probabilité de l’évènement C « l’élève interrogé est une fille joueuse dans une équipe ».
p(B)=\dfrac{12}{30}= 0,4
6. Cocher la bonne notation de l’évènement D « l’élève interrogé est une fille ou un(e) joueur(se) dans une équipe ».
\quad \Box A U B \quad \Box A x B \quad \Box A ∩ B
\quad \Box A U B \quad \Box A x B \quad \Box A ∩ B
\boxtimes A U B \quad \Box A ∩ B \quad \Box A x B
7. Calculer la probabilité de l’évènement D « l’élève interrogé est une fille ou un(e) joueur(se) dans une équipe ».
p(A U B) = p(A) + p(B) – p(A ∩ B)
p(D) = p(A) + p(B) – p(C) = 0,67 + 0,53 – 0,40 = 0,80
Autre Méthode :
Le nombre d’élèves concernés par l’évènement D est : 20 filles + 4 garçons joueurs = 24 élèves
p(D)=\dfrac{24}{30}= 0,80
p(D) = p(A) + p(B) – p(C) = 0,67 + 0,53 – 0,40 = 0,80
Autre Méthode :
Le nombre d’élèves concernés par l’évènement D est : 20 filles + 4 garçons joueurs = 24 élèves
p(D)=\dfrac{24}{30}= 0,80
Proba10. CCF exemple 1 : « Menu formule »
Enoncé
Un restaurateur vous propose un nouveau « menu formule » avec une entrée, un plat du jour et un désert. Le client a le choix entre :
– 3 entrées : œuf mimosa à 2 € – salade niçoise à 4 € – charcuterie à 7 €
– 2 plats du jour : steak frites à 10 € – saumon riz à 12 €
– 2 desserts : tarte aux pommes à 6 € – gâteau aux amandes à 8 €
– 3 entrées : œuf mimosa à 2 € – salade niçoise à 4 € – charcuterie à 7 €
– 2 plats du jour : steak frites à 10 € – saumon riz à 12 €
– 2 desserts : tarte aux pommes à 6 € – gâteau aux amandes à 8 €
1. Choisissez votre menu et calculer son prix.
Chacun aura sa propre réponse. Voici un exemple de menu choisi :
œuf mimosa + steak frites + tarte aux pommes
Tarif du menu choisi : 2 + 10 + 6 = 18 €
œuf mimosa + steak frites + tarte aux pommes
Tarif du menu choisi : 2 + 10 + 6 = 18 €
2. A l’aide d’un tableur, déterminer le prix de tous les menus différents qui peuvent être composés avec les trois entrées, les deux plats et les deux desserts.
3. Compter le nombre de repas à 22 € à l’aide de la formule suivante : « =NB.SI(plage cellules tarif;22) »
4. Le restaurateur envisage de proposer plus de possibilités à 22 €. Pour cela, il se propose de diminuer ou d’augmenter de 1 € un seul tarif parmi les trois entrées. Rechercher, à l’aide d’un tableur, le tarif de l’entrée qu’il faut modifier pour obtenir le maximum de menus à 22 €.
CCF 1. tableur2 diminution tarif
CCF 1. tableur2 augmentation tarif
Il faut faire baisser le tarif des charcuteries à 6 € pour obtenir 4 menus à 22 €.
CCF 1. tableur2 augmentation tarif
Il faut faire baisser le tarif des charcuteries à 6 € pour obtenir 4 menus à 22 €.
Enoncé
Une étude statistique a été réalisée sur le prix payé par les clients avec l’ancien « menu formule » durant les deux dernies mois. Les résultats sont présentés dans le tableau suivant :
| Prix en € | [17 ; 19[ | [19 ; 21[ | [21 ; 23[ | [23 ; 25[ | [25 ; 27[ |
| Effectif | 97 | 313 | 391 | 292 | 107 |
5. Déterminer les fréquences de chaque tarif, en pourcentage.
Rappel de la formule pour calculer une fréquence :
f=\dfrac{\text{nb cas favorables}}{\text{nb total de possibilités}} x 100
f=\dfrac{\text{nb cas favorables}}{\text{nb total de possibilités}} x 100
| Prix en € | [17 ; 19[ | [19 ; 21[ | [21 ; 23[ | [23 ; 25[ | [25 ; 27[ |
|---|---|---|---|---|---|
| Effectif | 97 | 313 | 391 | 292 | 107 |
| Fréquence en % | 8,08 | 26,08 | 32,58 | 24,33 | 8,92 |
6. En prenant au hasard la note d’un client dans cette étude statistique, calculer la probabilité des événements suivants :
Événement A : « le montant de la note est égal ou supérieur à 21 € »
Événement B : « le montant de la note est inférieur à 23 € »
Événement A : « le montant de la note est égal ou supérieur à 21 € »
Événement B : « le montant de la note est inférieur à 23 € »
Rappel de la formule pour calculer une probabilité :
p(A)=\dfrac{\text{nb d'issues favorables}}{\text{nb total d'issues possibles}}
p(A)=\dfrac{\text{nb d'issues favorables}}{\text{nb total d'issues possibles}}
On a 391 + 292 + 107 = 790 issues favorables pour 1200 issues possibles au total
p(A)=\dfrac{790}{1200}= 0,66
p(A)=\dfrac{790}{1200}= 0,66
On a 97 + 313 + 391 = 801 issues favorables pour 1200 issues possibles au total
p(B)=\dfrac{801}{1200}= 0,67
p(B)=\dfrac{801}{1200}= 0,67
7. Traduire par une phrase l’événement (A U B)
(A U B) : « le montant de la note est supérieur ou égal à 17 € et inférieur à 27 € »
ou bien
(A U B) : « le montant de la note est compris entre 17 € et 27 €, non inclus pour ce dernier tarif »
ou bien
(A U B) : « le montant de la note est compris entre 17 € et 27 €, non inclus pour ce dernier tarif »
8. Calculer la probabilité de l’événement (A U B).
Cet événement correspond à toutes les issues possibles pour les tarifs des menus, sa probabilité est donc de 1.
p( A U B) = 1
p( A U B) = 1
9. Calculer la probabilité de l’événement (A ∩ B).
Rappel de la formule :
p(A U B) = p(A) + p(B) – p(A ∩ B)
p(A U B) = p(A) + p(B) – p(A ∩ B)
p(A ∩ B) = p(A) + p(B) – p(A U B) = 0,66 + 0,67 – 1 = 0,33
10. Traduire par une phrase l’événement (A ∩ B)
(A ∩ B) : « le montant de la note est supérieur ou égal à 21 € et inférieur à 23 € »
ou bien
(A ∩ B) : « le montant de la note est compris entre 21 € et 23 €, non inclus pour ce dernier tarif »
ou bien
(A ∩ B) : « le montant de la note est compris entre 21 € et 23 €, non inclus pour ce dernier tarif »
11. Le restaurateur décide finalement de proposer des charcuteries à 6 €. Les tarifs proposés alors sur la nouvelle carte seront-ils adaptés à la clientèle de ce restaurant, si les résultats de l’étude statistique sont représentatifs de cette clientèle. Justifier votre réponse.
On réalise un tableau des tarifs des menus et de leur effectif respectif avec les charcuteries à 6 € (trouvés à l’aide du tableur 2). Puis on calcule les fréquences des tarifs. Si les fréquences sont proches de celles de la question 5 alors les tarifs seront adaptés à la clientèle.
| Prix en € | [17 ; 19[ | [19 ; 21[ | [21 ; 23[ | [23 ; 25[ | [25 ; 27[ |
|---|---|---|---|---|---|
| Effectif | 1 | 3 | 4 | 3 | 1 |
| Fréquence en % | 8,08 | 25,00 | 33,33 | 25,00 | 8,08 |
Les fréquences des deux propositions, ancien et nouveau tarif des charcuteries, sont proches. Ces nouveaux tarifs sont donc adaptés à la clientèle du restaurant.
SG2 – Correction de l’interrogation – Devoir B
Vocabulaire des suites géométriques
1. Quelle est l’opération mathématique réalisée pour passer d’un terme à un autre pour une suite géométrique ?
\boxtimes multiplication \quad \Box addition \quad \Box division \quad \Box soustraction
La multiplication pour une suite géométrique
La multiplication pour une suite géométrique
2. Quelle est la formule avec le terme de rang n et le terme suivant pour une suite géométrique ?
\boxtimes u_{n+1}=u_{n} \times q \quad \Box u_{n}=u_{n+1} \times r
\Box u_{n}=u_{n+1}+r \quad \Box u_{n}=u_{n+1} \times r
Pas de r pour une suite géométrique
\Box u_{n}=u_{n+1}+r \quad \Box u_{n}=u_{n+1} \times r
Pas de r pour une suite géométrique
3. Quelles sont les 2 formules faisant apparaître u_n , u_0 ou u_1 et q pour une suite géométrique ?
\Boxu_{n}=u_{0} \times q^{n-1}\quad \boxtimes u_{n}=u_{1} \times q^{n-1}
\Boxu_{n}=u_{1} \times q^n \quad \boxtimes u_{n}=u_{0} \times q^n
N’oubliez pas que u_{1}=u_{0} \times q
\Boxu_{n}=u_{1} \times q^n \quad \boxtimes u_{n}=u_{0} \times q^n
N’oubliez pas que u_{1}=u_{0} \times q
4. Quelle est l’opération mathématique réalisée pour une diminution de 12% ?
\Box 1,12 \quad \boxtimes 0,88 \quad \Box 0,12 \quad \Box -0,12
Réduction ou diminution 1-t%=1-0,12=0,88
Réduction ou diminution 1-t%=1-0,12=0,88
5. Quelle est l’opération mathématique réalisée pour une augmentation de 31% ?
\Box 0,69 \quad \boxtimes 1,31 \quad \Box 0,31 \quad \Box -0,31 \quad
Augmentation ou croissance 1+t%=1+0,31=1,31
Calcul des termes d’une suite géométrique connaissant u_{0} ou u_{1} et q
(u_{n}) est une suite géométrique de raison q
(u_{n}) est une suite géométrique de raison q
1. On donne u_{0}=2 et q=3, calculer u_{3}.
u_{n}=u_{0} \times q^n=2 \times 3^n
u_{3}=2 \times 3^3=54
u_{3}=2 \times 3^3=54
2. On donne u_{0}=5 et q=-2, calculer u_{5}.
u_{n}=u_{0} \times q^n=5 \times (-2)^n
u_{5}=5 \times (-2)^5=-160
u_{5}=5 \times (-2)^5=-160
3. On donne u_{0}=-3 et q=4, calculer u_{4}.
u_{n}=u_{0} \times q^n=(-3) \times 4^n
u_{4}=(-3) \times 4^4=324
u_{4}=(-3) \times 4^4=324
4. On donne u_{1}=4 et q=-3, calculer u_{3}.
u_{n}=u_{1} \times q^{n-1}=4 \times (-3)^{n-1}
u_{3}=4 \times (-3)^{3-1}=36
u_{3}=4 \times (-3)^{3-1}=36
5. On donne u_{1}=5 et q=2/3, calculer u_{4}.
u_{n}=u_{1} \times q^{n-1}=5 \times (2/3)^n
u_{4}=5 \times (2/3)^{4-1}=1,48
u_{4}=5 \times (2/3)^{4-1}=1,48
SG20 – Devoir A
Vocabulaire des suites géométriques
1. Quelle est l’opération mathématique réalisée pour passer d’un terme à un autre pour une suite géométrique ?
\Box addition \quad \Box division \quad \Box soustraction \quad \boxtimes multiplication
La multiplication pour une suite géométrique
La multiplication pour une suite géométrique
2. Quelle est la formule avec le terme de rang n et le terme suivant pour une suite géométrique ?
\Box u_{n+1}=u_n \times r \quad \Box u_{n}=u_{n+1} \times r
\Box u_{n}=u_{n+1}+r \quad \boxtimes u_{n+1}=u_{n} \times q
Pas de r pour une suite géométrique
\Box u_{n}=u_{n+1}+r \quad \boxtimes u_{n+1}=u_{n} \times q
Pas de r pour une suite géométrique
3. Quelles sont les 2 formules faisant apparaître u_n , u_0 ou u_1 et q pour une suite géométrique ?
\Box u_{n}=u_{1} \times q^n \quad \boxtimes u_{n}=u_{0} \times q^n
\Boxu_{n}=u_{0} \times q^{n-1} \quad \boxtimes u_{n}=u_{1} \times q^{n-1}
N’oubliez pas que u_{1}=u_{0} \times q
\Boxu_{n}=u_{0} \times q^{n-1} \quad \boxtimes u_{n}=u_{1} \times q^{n-1}
N’oubliez pas que u_{1}=u_{0} \times q
4. Quelle est l’opération mathématique réalisée pour une diminution de 11% ?
\Box 0,11 \quad \Box 1,11 \quad \boxtimes 0,89 \quad \Box -0,11 \quad
Réduction ou diminution 1-t%=1-0,11=0,89
Réduction ou diminution 1-t%=1-0,11=0,89
5. Quelle est l’opération mathématique réalisée pour une augmentation de 13% ?
\Box 0,13 \quad \boxtimes 1,13 \quad \Box 0,87 \quad \Box -0,13 \quad
Augmentation ou croissance 1+t%=1+0,13=1,13
Calcul des termes d’une suite géométrique connaissant u_{0} ou u_{1} et q
(u_{n}) est une suite géométrique de raison q
(u_{n}) est une suite géométrique de raison q
1. On donne u_{0}=3 et q=2, calculer u_{3}.
u_{n}=u_{0} \times q^n=3 \times 2^n
u_{3}=3 \times 2^3=24
u_{3}=3 \times 2^3=24
2. On donne u_{0}=-2 et q=5, calculer u_{5}.
u_{n}=u_{0} \times q^n=(-2) \times 5^n
u_{5}=(-2) \times 5^5=-6250
u_{5}=(-2) \times 5^5=-6250
3. On donne u_{0}=4 et q=-3, calculer u_{4}.
u_{n}=u_{0} \times q^n=4 \times (-3)^n
u_{4}=4 \times (-3)^4=324
u_{4}=4 \times (-3)^4=324
4. On donne u_{1}=4 et q=-3, calculer u_{3}.
u_{n}=u_{1} \times q^{n-1}=4 \times (-3)^{n-1}
u_{3}=4 \times (-3)^{3-1}=36
u_{3}=4 \times (-3)^{3-1}=36
5. On donne u_{1}=5 et q=2/3, calculer u_{4}.
u_{n}=u_{1} \times q^{n-1}=5 \times (2/3)^n
u_{4}=5 \times (2/3)^{4-1}=1,48
u_{4}=5 \times (2/3)^{4-1}=1,48
SG05 – Somme des termes : Application de la formule
Définition :
La somme des n premiers termes d’une suite géométrique peut être déterminé avec la formule suivante :
S=u_0 \times \dfrac{q^{n+1}-1}{q-1}
ou
S=u_1 \times \dfrac{q^{n}-1}{q-1}
Attention une formule avec u_0 et une autre avec u_1 !!!
S=u_0 \times \dfrac{q^{n+1}-1}{q-1}
ou
S=u_1 \times \dfrac{q^{n}-1}{q-1}
Attention une formule avec u_0 et une autre avec u_1 !!!
Pour appliquer la formule de calcul de somme de n termes d’une suite géométrique, il faut :
- Déterminer le nombre de termes n de la suite.
- Connaître le premier terme et la raison.
- Appliquer la formule avec u_0 ou u_1
Exemple avec u_0 :
Calculer la somme de 5 premiers termes de la suite géométrique avec u_0=2 et q=3
Ici, n=5 et on applique la formule avec u_0.
Ainsi S=u_0 \times \dfrac{q^{n+1}-1}{q-1}
Ou S=2 \times \dfrac{3^{5+1}-1}{3-1}
Enfin S=2 \times \dfrac{729-1}{3-1}=2 \times \dfrac{728}{2}=728
On vérifie : S=u_0+u_1+u_2+u_3+u_4+u_5
S=(2)+(6)+(18)+(54)+(162)+(486)=728
Exemple avec u_1 :
Calculer la somme de 3 premiers termes de la suite géométrique avec u_1=-2 et q=2
Ici, n=3 et on applique la formule avec u_1.
Ainsi S=u_1 \times \dfrac{q^{n}-1}{q-1}
Ou S=(-2) \times \dfrac{2^{3}-1}{2-1}
Enfin S=(-2) \times \dfrac{8-1}{2-1}=(-2) \times \dfrac{7}{1}=-14
On vérifie : S=u_1+u_2+u_3=(-2)+(-4)+(-8)=-14
Exercices :
Calculer la somme de 10 premiers termes de la suite géométrique avec u_0=100 et q=2
Calculer la somme de 10 premiers termes de la suite géométrique avec u_1=20000 et q=1,05
SG8 – Exercices en ligne
Liens :
- Homeomath
- qcmdemath.net
- digiSchool
Encore faire la différence entre suite arithmétique et géométrique
Attention faire les exercices de 7 à 12 sur les suites géométriques, les premiers exercices sont sur les suites arithmétiques.
SG9a – Etablir un tableau d’amortissement – Amortissement constant
Le directeur de l’entreprise Les transporteurs réunis envisage l’achat d’un nouveau véhicule destiné au transport des marchandises. Pour financer cet achat, l’entreprise va devoir contracter l’emprunt d’un capital de 50 000 € au taux de 3,8 % par an remboursable en cinq annuités.
Avant de prendre sa décision, il demande à son comptable d’établir un tableau récapitulatif des remboursements de cet emprunt.
A. Amortissement constant
Le comptable propose un remboursement avec un amortissement constant et doit compléter le tableau d’amortissement ci-dessous, où les montants sont en euros.
| Echéances | Capital dû avant l’échéance | Amortissement | Intérêts | Annuités |
| 1 | 50000 | |||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
L’amortissement est la part de capital remboursé.
L’amortissement constant A d’un capital de valeur V_0 remboursé en n annuités est égal à : A=\dfrac{V_0}{n}
L’amortissement constant A d’un capital de valeur V_0 remboursé en n annuités est égal à : A=\dfrac{V_0}{n}
1. Calculer le montant de l’amortissement constant, puis compléter la troisième colonne.
A=\dfrac{V_0}{n}=\dfrac{50000}{5}=10000
Pour une échéance donnée, le capital restant dû est égal à la différence du capital dû l’année précédente et de l’amortissement.
2. Remplir la deuxième colonne avec le capital dû
C_1=50000
C_2=40000
C_3=30000
C_4=20000
C_5=10000
Les intérêts représentent 3,8 % du capital restant dû avant l’échéance.
3. Calculer l’intérêt pour chaque échéance, puis compléter la quatrième colonne du tableau.
i_1=50000 \times 0,038=1900
i_2=40000 \times 0,038=1520
i_3=30000 \times 0,038=1140
i_4=20000 \times 0,038=760
i_5=10000 \times 0,038=380
L’annuité est la somme de l’amortissement et de l’intérêt.
4. Calculer le montant de la première annuité, puis compléter la cinquième colonne.
première annuité = 10 000 + 1 900 = 11 900
5. Quelle est la nature de la suite formée par les différentes annuités. Préciser son premier terme et sa raison.
11900 – 11520 = 11520 – 11140 = 11140 – 10760 = 10760 – 10380 = 380
Il s’agit donc d’une suite arithmétique de premier terme 11 900 et de raison r = – 380
SG9b – Etablir un tableau d’amortissement – Annuités constantes
Le directeur de l’entreprise Les transporteurs réunis envisage l’achat d’un nouveau véhicule destiné au transport des marchandises. Pour financer cet achat, l’entreprise va devoir contracter l’emprunt d’un capital de 50 000 € au taux de 3,8 % par an remboursable en cinq annuités.
Avant de prendre sa décision, il demande à son comptable d’établir un tableau récapitulatif des remboursements de cet emprunt.
B. Annuités constantes
Le remboursement par amortissement constant ne convient pas au directeur de l’entreprise : il préfèrerait 5 annuités de même montant pour rembourser son emprunt de 50 000 € au taux de 3,8 %. Le comptable utilise un tableur pour réaliser le tableau d’amortissement comme représenté ci-dessous.
| Echéances | Capital restant dû | Amortissement | Intérêts | Annuités |
| 1 | 50000 | |||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
Les fonctions financières du tableur permettent les calculs d’annuités et d’intérêts de remboursement d’emprunts.
La fonction financière =VPM(taux;npm;va)
du tableur permet le calcul de l’annuité pour un emprunt à taux constant (taux), connaissant le nombre d’annuités de remboursement (npm) et le capital emprunté (va).
du tableur permet le calcul de l’annuité pour un emprunt à taux constant (taux), connaissant le nombre d’annuités de remboursement (npm) et le capital emprunté (va).
1. Calculer l’annuité en saisissant dans la cellule E2 la formule : =VPM(3,8%;5;50000). Compléter la colonne Annuité du tableau sachant que le directeur souhaite une annuité constante.
Noter la valeur obtenue, sans tenir compte du signe négatif qui indique qu’il s’agit d’une somme due.
première annuité = 11 168,33 €
La fonction financière =INTPER(taux;per;npm;va) du tableur permet le calcul de l’intérêt pour une période donnée.
Les intérêts représentent 3,8 % du capital restant dû avant l’échéance.
Les intérêts représentent 3,8 % du capital restant dû avant l’échéance.
2. Calculer l’intérêt de la première échéance en saisissant dans la cellule D2 la formule : =INTPER(3,8%;1;5;B2).
Noter la valeur obtenue, sans tenir compte du signe négatif qui indique qu’il s’agit d’une somme due.
premier intérêt = 1 900 €
3. Saisir dans la cellule C2 la formule =E2-D2 et noter la valeur obtenue :
On rappelle que l’amortissement est égal au montant de l’annuité moins l’intérêt.
premier amortissement = 9 268,33 €
4. Saisir dans la cellule B3 la formule =B2+C2 (attention la valeur de l’amortissement donnée par la tableur est négative) et noter la valeur obtenue :
Le capital restant dû à la deuxième échéance est égal au capital de l’échéance précédente moins l’amortissement.
capital restant dû = 40 731,67 €
5. Compléter la 2ème ligne du tableau d’amortissement en recopiant la cellule Intérêt, puis Amortissement, et enfin Capital restant dû à l’échéance 3.
6. Répéter ces opérations, ligne par ligne, pour compléter l’ensemble du tableau.
7. Effectuer la somme des différents amortissements.
50 000 €
8. Comparer la somme obtenue avec le montant du capital emprunté.
La somme des amortissements est égale au capital emprunté.
9. Quelle est la nature de la suite formée par les différents amortissements. Préciser son premier terme et sa raison.
9620,52 / 9268,33 = 9986,10 / 9620,52 = 10365,58 / 9986,10 = 10365,58 / 10365,58 = 1,038
Il s’agit donc d’une suite géométrique de premier terme 9 268,33 et de raison q = 1,038.
Il s’agit donc d’une suite géométrique de premier terme 9 268,33 et de raison q = 1,038.