Fonction dérivée et étude des variations d’une fonction

FD06 – Tableau de variation

Afin de résumer toutes les variations d’une fonction, il faut élaborer un tableau de variation.
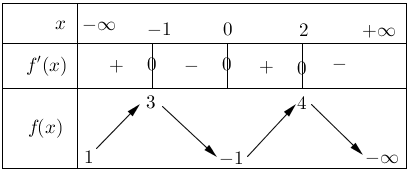
interactiff20
① Ce tableau se base sur l’ensemble de définition I de la fonction qui vous sera donné.
Dans ce tableau de variation doit figurer les abscisses de I ainsi que les valeurs particulières qui annulent la dérivée.

x -\infty -1 0 2 +\infty

﹖⃝Ici l’ensemble de définition est ]-\infty;+\infty[ avec 3 valeurs particulières -1;0;2.
—————–
② On doit y trouver aussi une étude du signe de la dérivée.

f'(x) + 0 - 0 +

﹖⃝Ici le signe de la dérivée change aux valeurs particulières -1;0;2.
—————–
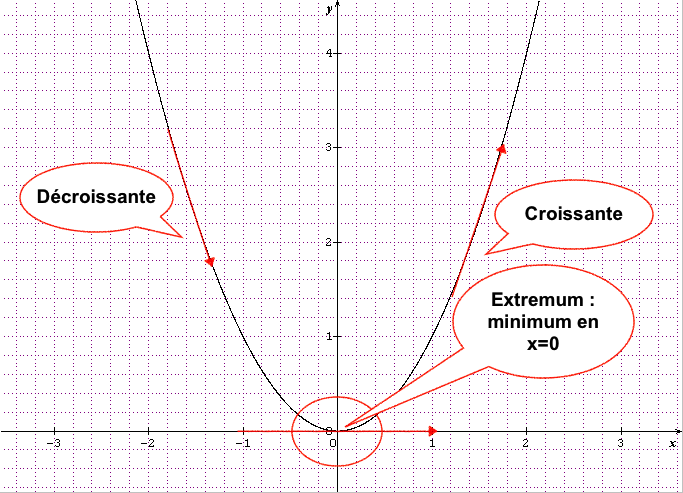
③ Et enfin les variations de la fonction symbolisées par des flèches.
On en conclut les variations de la fonctions avec des flèches montantes pour de la croissance, descendante pour de la décroissance et horizontale pour la constance.
⚠ N’oubliez d’inscrire les valeurs des images des valeurs particulières par la fonction f.












Tableau de variation de la fonction f(x)=3x^2+12x-5 définie sur l’intervalle I=[-5;2]
① On calcule la dérivée de la fonction f : f'(x)=6x+12
② On résout l’équation f'(x)=0 : 6x+12=0 ou x=-2
La dérivée s’annule donc en -2, la fonction change de signe en ce point.
③ On étudie le signe de la dérivée de f :
f'(x)>0 quand x>-2
f'(x)<0 quand x<-2 On résume :
f'(x) - 0 +

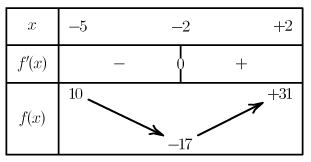
④ On calcule les valeurs des images des valeurs particulières.
f(-5)=3(-5)^2+12(-5)-5=10
f(-2)=3(-2)^2+12(-2)-5=-17
f(2)=3(2)^2+12(2)-5=31
⑤ On construit les flèches associées aux signes de la dérivées.
⑥ On obtient :
tdv-01


① Réaliser le tableau de variation de la fonction f(x)=-x^2+3x-2 sur I=[-1;4]
② Réaliser le tableau de variation de la fonction f(x)=x^2+4x-2 sur I=[-4;1]
Fonction dérivée et étude des variations d’une fonction

FD05 – Applications à l’étude des variations d’une fonction

Signe de la dérivée et variations
Soit f une fonction dérivable sur un intervalle I :

Si f'(x)>0 alors la fonction est croissante sur I.
Si f'(x)=0 alors la fonction est constante sur I.
Si f'(x)<0 alors la fonction est décroissante sur I.

Soit f une fonction dérivable sur un intervalle I.
Si f(x)=2x alors f'(x)=2 or f'(x)>0 donc f est croissante.
Soit f une fonction dérivable sur un intervalle I.
Si f(x)=-3x alors f'(x)=-3 or f'(x)<0 donc f est décroissante.


Recherche d’extremum
SI pour une valeur x_0 appartenant à l’intervalle I, f'(x_0) s’annule en changeant de signe alors la fonction f passe par un extremum (minimum ou maximum) pour x=x_0.

Soit f une fonction dérivable sur un intervalle I telle que f(x)=x^2.
f'(x)=2x
Si x<0 alors f'(x)<0 donc la fonction est décroissante.
Si x=0 alors f'(x)=0 donc la fonction est constante.
Si x>0 alors f'(x)>0 donc la fonction est croissante.
La fonction f(x)=x^2 s’annule en x_0=0 en changeant de signe donc x_0=0 est un extremum ici un minimum.

carré




1.Soit f une fonction dérivable sur un intervalle I=[-2;2] telle que f(x)=-3x^2.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
2.Soit f une fonction dérivable sur un intervalle \mathbb{R} telle que f(x)=-4x^3.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
3.Soit f une fonction dérivable sur un intervalle \mathbb{R^+*} telle que f(x)=-\sqrt{x}.
A l’aide du calcul de la dérivée, déterminer les variations de la fonction f.
4.Soit f une fonction dérivable sur un intervalle I=[1;7] telle que f(x)=\dfrac{-3}{x}.
A l’aide du calcul de la dérivée, déterminer un extremum.

5.Soit f une fonction dérivable sur un intervalle I=[-1;3] telle que f(x)=x^2-2x+1.
A l’aide du calcul de la dérivée, déterminer un extremum.

Fonction dérivée et étude des variations d’une fonction

FD04 – QCM Dérivées

Cliquer sur le bouton « Départ » pour commencer le QCM

QCM Dérivées

Calculez les dérivées des fonctions suivantes
Départ

Félicitation - vous avez complété QCM Dérivées.

Vous avez obtenu %%SCORE%% sur %%TOTAL%%.

Votre performance a été évaluée à %%RATING%%


Vos réponses sont surlignées ci-dessous.
Retour
Les questions en gris sont complétées.
12345
678Fin
Retour

Fonction dérivée et étude des variations d’une fonction

FD03B – Exercices calcul de dérivées

① Calculer la dérivée de f(x)=-3x
f'(x)=-3 -> Fonction affine + règle kf
② Calculer la dérivée de f(x)=-2x^2
f'(x)=-4x -> Fonction carrée + règle kf
③ Calculer la dérivée de f(x)=\dfrac{-6}{x}
f'(x)=\dfrac{6}{x^2} -> Fonction inverse + règle kf
④ Calculer la dérivée de f(x)=6\sqrt{x}
f'(x)=\dfrac{6}{2\sqrt{x}}=\dfrac{3}{\sqrt{x}} -> Fonction racine carrée + règle kf
⑤ Calculer la dérivée de f(x)=3x^2+5x-2
f'(x)=6x+5 -> règle f+g
⑥ Calculer la dérivée de f(x)=-x^3+8x+12
f'(x)=-3x^2+5 -> règle f+g
⑦ Calculer la dérivée de f(x)=x^3-2x^2+3x-9
f'(x)=3x^2-4x+3 -> règle f+g
⑧ Calculer la dérivée de f(x)=\dfrac{3x^2+2x-2}{x}
f(x)=\dfrac{3x^2}{x}+\dfrac{2x}{x}-\dfrac{2}{x}
f(x)=3x+2-\dfrac{2}{x}
f'(x)=3+\dfrac{2}{x^2} -> règle f+g

⑨ Calculer la dérivée de f(x)=(x-2)(-x+5)
f(x)=-x^2+5x+2x-10
f(x)=-x^2+7x-10
f'(x)=-2x+7 -> règle f+g

⑩ Calculer la dérivée de f(x)=4\sqrt{x}(\sqrt{x}+2)
f(x)=4\sqrt{x} \times \sqrt{x}+4\sqrt{x} \times 2
f(x)=4x+8\sqrt{x}
f'(x)=4+\dfrac{4}{\sqrt{x}} -> règle f+g

Fonction dérivée et étude des variations d’une fonction

FD-03A : Exercices calcul de dérivées

① Calculer la dérivée de f(x)=-5x
② Calculer la dérivée de f(x)=\dfrac{1}{2}x^2
③ Calculer la dérivée de f(x)=4x^3
④ Calculer la dérivée de f(x)=-\dfrac{1}{3}x^3
⑤ Calculer la dérivée de f(x)=\dfrac{3}{x}
⑥ Calculer la dérivée de f(x)=x+\dfrac{1}{x}
⑦ Calculer la dérivée de f(x)=x^2-5x+1
⑧ Calculer la dérivée de f(x)=x^3+2x+1
⑨ Calculer la dérivée de f(x)=2x^2-\dfrac{1}{x}
⑩ Calculer la dérivée de f(x)=x^3+5x^2+4x+3
⑪ Calculer la dérivée de f(x)=(x+1)(x+2)
⑫ Calculer la dérivée de f(x)=\dfrac{4x^2+1}{x}
Fonction dérivée et étude des variations d’une fonction

FD02 – Calcul de dérivées

Fonction dérivable sur un intervalle I
Étant donnée une fonction f dérivable sur un intervalle I, la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction f en x est appelée fonction dérivée de la fonction f sur I et est notée f'.
Un intervalle I peut se présenter sous différentes sortes : I=[0;5], I=]-\infty;5] ou encore I=]-2;+\infty[.
I=\mathbb{R} représente l’ensemble des réels et I=\mathbb{R}^+ représente l’ensemble des réels positifs.
Tableau récapitulatif des dérivées usuelles

Fonction Expression Fonction dérivée
Constante a 0
Affine ax+b a
Carrée x^2 2x
Cube x^3 3x^2
Inverse \dfrac{1}{x} -\dfrac{1}{x^2}
Racine carrée \sqrt{x} \dfrac{1}{2\sqrt{x}}
Si f(x)=4 alors f'(x)=0 => Fonction constante
Si f(x)=2x alors f'(x)=2 => Fonction linéaire
Si f(x)=2x+4 alors f'(x)=2 => Fonction affine (=fonction linéaire + fonction constante)
Si f(x)=x^2 alors f'(x)=2x => Fonction carrée
Si f(x)=x^3 alors f'(x)=3x^2 => Fonction cube
Si f(x)=\dfrac{1}{x} alors f'(x)=-\dfrac{1}{x^2} => Fonction inverse
Si f(x)=\sqrt{x} alors f'(x)=\dfrac{1}{2\sqrt{x}} => Fonction racine carrée






Règles de dérivation 1 : Fonction multipliée par un réel
Étant donnée deux fonctions f et h dérivables sur un intervalle I et un réel k telles que h=k \times f et , la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction h en x est appelée fonction dérivée de la fonction h sur I et est notée h' et est égale à k \times f'.
Si h(x)=2x alors on peut écrire h(x)=k \times f(x) avec k=2 et f(x)=x or f'(x)=1.
On en déduit que h'(x)=k \times f'(x)=2 \times 1=2.
Si h(x)=3x^2 alors on peut écrire h(x)=k \times f(x) avec k=3 et f(x)=x^2 or f'(x)=2x.
On en déduit que h'(x)=k \times f'(x)=3 \times 2x=6x.
Si h(x)=5\sqrt{x} alors on peut écrire h(x)=k \times f(x) avec k=5 et f(x)=\sqrt{x} or f'(x)=\dfrac{1}{2\sqrt{x}}.
On en déduit que h'(x)=k \times f'(x)=5 \times \dfrac{1}{2\sqrt{x}}=\dfrac{5}{2\sqrt{x}}.

Règles de dérivation 2 : Addition de deux fonctions
Étant donnée trois fonctions f,g et h dérivables sur un intervalle I et telles que h=f+g, la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction h en x est appelée fonction dérivée de la fonction h sur I et est notée h' et est égale à f'+g'.
Si h(x)=2x+4 alors on peut écrire h(x)=f(x)+g(x) avec f(x)=2x et g(x)=4
or f'(x)=2 et g'(x)=0. On en déduit que h'(x)=f'(x)+g'(x)=2+0=2.
Si h(x)=x^3+x^2 alors on peut écrire h(x)=f(x)+g(x) avec f(x)=x^3 et g(x)=x^2
or f'(x)=3x^2 et g'(x)=2x. On en déduit que h'(x)=f'(x)+g'(x)=3x^2+2x.
Si h(x)=\dfrac{1}{x}+2x alors on peut écrire h(x)=f(x)+g(x) avec f(x)=\dfrac{1}{x} et g(x)=2x
or f'(x)=\dfrac{1}{2\sqrt{x}} et g'(x)=2. On en déduit que h'(x)=f'(x)+g'(x)=\dfrac{1}{2\sqrt{x}}+2.
Lors de plusieurs additions de fonctions, on applique la règle sur la dérivée de l’addition de deux fonctions plusieurs fois.
h(x)=2x^3-x^2+3x-2 donne h'(x)=6x^2-2x+3
Fonction dérivée et étude des variations d’une fonction, Terminale

FD01 : Approche de la dérivée

Pour étudier les variations d’une fonction, nous avions jusqu’ici la possibilité de réaliser :
– à partir de son expression algébrique
f(x)=2x^3+2
– sa représentation graphique :
fonction01
– et son tableau de valeurs :
tableau01
Quoi de neuf en terminale ?



Prenons ce rugbyman qui tape dans un ballon :
rudby01
Plusieurs trajectoires sont possibles :
rudby02
La trajectoire peut être modélisée par une fonction numérique. Cette année, nous allons pouvoir prévoir les variations de la fonction numérique (ici la trajectoire).
rudby03
On va s’aider des tangentes en plusieurs points à la trajectoire du ballon.
rudby04
Pour être plus précis, on va multiplier les points de la trjectoire…
rudby05
et calculer les tangentes.
rudby0
On a donc réussi à affiner la trajectoire du ballon.
rudby06

Toute représentation graphique peut être approchée par une succession de tangentes en chaque point de la courbe.
Les tangentes sont intéressantes car ce sont des droites donc faciles à étudier en mathématiques.
Les droites,représentations graphiques, ont été étudiées en seconde par leur fonction, la fonction affine f(x)=ax+b.
Une droite se caractérise avant tout par son coefficient directeur a qui nous indique si la droite est croissante ou décroissante.

Revenons une dernière fois sur notre rugbyman :
On voit que les tangentes ont un coefficient directeur positif quand la trajectoire monte et qu’elles ont un coefficient directeur négatif quand la trajectoire descend.
rudby07

De plus lorsqu’on arrive au sommet de la trajectoire, le coefficient directeur de la tangente parallèle au sol (axe des abscisses) est nul.

Connaître le signe des coefficients directeurs des tangentes permet donc de déterminer les variations de la trajectoire.
– signe positif : trajectoire croissante
– signe nul : trajectoire constante
– signe négatif : trajectoire décroissante
C’est ce coefficient directeur de tangente que l’on appellera maintenant le nombre dérivé.
Il y autant de nombres dérivées que de tangentes possibles en chaque point de la courbe.
L’ensemble des nombres dérivés sont obtenus grâce à la fonction dérivée de la fonction numérique étudiée.

x \mapsto f'(x)

On dit « f prime de x ».

Suites géométriques

SG-10 – Salle de concert

Pour la location d’une salle de concert, la municipalité pratique un tarif dégressif suivant la durée de la prestation.
Elle demande 3570€ la première journée et facture chaque journée supplémentaire 15% de moins que la précédente.
Jerry est manager de groupes musicaux et souhaite louer la salle pour des festivals.


On fixe u_n la suite représentant le coût des journées.

1. Combien coûte la première journée.
u_1=3570
2. Combien coûte la seconde journée.
u_2=u_1 \times q
Une réduction de 15% correspond à un facteur multiplicateur de 100\%-15\%=85\%=\dfrac{85}{100}=0,85.
u_2=3570 \times 0,85=3034,50
La seconde journée coutera donc 3034,50€.
3. Combien coûte la troisième journée.
u_3=u_2 \times q
u_2=3034,50 \times 0,85=2579,325
La seconde journée coutera donc 2579,325€.
3. Déterminer la nature de la suite et sa raison.
Faire attention à ne pas arrondir les valeurs de u_2 et u_3.
\dfrac{u_2}{u_1}=\dfrac{u_3}{u_2}=q
La suite u_n est une suite géométrique de raison q=0,85.
4. Déterminer u_n en fonction de n.
u_n=u_1 \times q^{n-1}
u_n=3570 \times 0,85^{n-1}
5. Déterminer le coût du 7ème jour de location de la salle de concert.
u_7=3570 \times 0,85^{7-1}
u_7=3570 \times 0,85^{6}
u_7=1346,42377078125






6. Combien de jours faut-il rester pour que la location de la salle coûte moins de 30€ .
Sur un tableur, on inscrit les indices et les prix dégressifs par jour et on s’aperçoit que le 31ème jour est en dessous de 30€.
u_31=3570 \times 0,85^{30}
u_31=27,24
7. Jerry veut organiser un premier concert en mars sur 4 jours. Combien va-t-il débourser pour ces 4 jours en arrondissant à l’unité.
S=u_1 \times \dfrac{0,85^{n}}{0,85-1}
S=3570 \times \dfrac{0,85^{4}}{0,85-1}
S=11376,2513
8. Jerry veut organiser un festival en juillet dans cette salle sur 7 jours. Combien va-t-il débourser pour ces 7 jours en arrondissant à l’unité.
S=u_1 \times \dfrac{0,85^{n}}{0,85-1}
S=3570 \times \dfrac{0,85^{7}}{0,85-1}
S=16170,2653
Suites géométriques

SG09 – Acheter ou louer

Faty et Jacques, deux jeunes parents, cherchent à déménager pour avoir plus d’espace et se rapprocher du centre-ville. Une agence immobilière leur propose un logement dont le loyer mensuel est de 720 € avec une augmentation prévisionnelle, liée à l’indice ICC, estimée à 3 % par an.
L’agence les informe que la propriétaire serait également disposée à leur vendre le bien pour 190 000 € (frais d’agence inclus). Envisageant de rester une vingtaine d’années dans cet appartement, le couple se demande s’il ne serait pas préférable d’acheter plutôt que de louer.

Jacques et Faty souhaitent connaître le montant total des loyers qu’ils auront à verser en 20 ans de location.


1. Proposer une méthode et un outil de résolution de cette situation problème.
– Il faut déterminer le montant total des loyers sur 20 années et comparer cette somme avec le montant de la vente soit 190 000 €.
– Pour cela il faut déterminer le montant annuel des loyers qui sera le premier terme de la suite géométrique de raison q = 1,03 (augmentation de 3%).
– Ensuite il faut calculer la somme des 20 premiers termes de cette suite.
– On vérifie à l’aide d’un tableur ou de la calculatrice.


2. Mettre en œuvre votre méthode de résolution.

2.a. Identifier le premier terme et la raison de cette suite géométrique.
Premier terme de la suite : u_1=12 \times 720=8640
Annuellement, Jacques et Faty vont payer 8640€.
Une augmentation de 3% est égale à un facteur multiplicateur 100%+3%=103%=1,03.
Raison de la suite : q=1,03


2.b. Déterminer le prix des loyers de la deuxième année u_2.
u_2=u_1 \times 1.03=8899.2
Le prix du loyer sera la deuxième année de 8899,20€.


2.c. Ecrire u_n en fonction de n.
u_n=u_1 \times q^n-1
u_n=8640 \times 1,03^n-1








2.d. Déterminer u_10 en arrondissant au centième près.
u_n=u_1 \times q^n-1
u_10=8640 \times 1,03^10-1
u_10=8640 \times 1,03^9
u_10=11273,24


2.e. Déterminer la somme des 20 premiers termes de la suite.
Nombres de termes : 20
Premier terme : u_1=8640
Raison : q=1,03
Sommes des termes :
S=u_1 \times \frac{q^n-1}{q-1}=8640 \times \frac{1,03^{20}-1}{1,03-1}
S=232160,04


2.f. Vérifier le calcul de la somme à l’aide d’un tableur.


2.g. Conclure : quelle est la meilleure option : 20 ans de loyers ou l’achat ?
Le montant total des 20 années de loyer (232 160,04 €) est supérieur au prix de vente de l’appartement (190 000 €).
Faty et Jacques ont donc plutôt intérêt à acheter l’appartement.
Suites géométriques

SG08 – Interrogation

Vocabulaire des suites géométriques
1. Quelles sont les 2 formules faisant apparaître u_n , u_0 ou u_1 et q pour une suite géométrique ?
\Box u_{n}=u_{1} \times q^n \Box u_{n}=u_{0} \times q^n
\Box u_{n}=u_{0} \times q^{n-1} \Box u_{n}=u_{1} \times q^{n-1}
2. Quelle est l’opération mathématique réalisée pour une diminution de 7% ?
diminution :
1-t%=1-7%=1-0,07=0,93
3. Quelle est l’opération mathématique réalisée pour une augmentation de 4% ?
augmentation :
1+t%=1+4%=1+0,04=1,04
4. Quelles sont les 2 formules de la somme des n premiers termes avec u_0 et u_1 pour une suite géométrique ?
\Box S=u_0 \times \dfrac{q^{n+1}-1}{q-1} \Box S=u_1 \times \dfrac{q^{n-1}-1}{q-1}
\Box S=u_0 \times \dfrac{q^{n}-1}{q-1} \Box S=u_1 \times \dfrac{q^{n}-1}{q-1}
Calcul des termes d’une suite géométrique connaissant u_{0} ou u_{1} et q
(u_{n}) est une suite géométrique de raison q
5. On donne u_{0}=200 et q=1,1, calculer u_{3}.
u_{n}=u_{0} \times q^n
u_{n}=200 \times {1,1}^n
u_{3}=200 \times {1,1}^3
u_{3}=266,2










6. On donne u_{1}=800 et q=0,87, calculer u_{6}.
u_{n}=u_{1} \times q^{n-1}
u_{n}=800 \times {0,87}^{n-1}
u_{6}=800 \times {0,87}^{6-1}
u_{6}=800 \times {0,87}^5
u_{6}=398,74
Calcul de la somme de n premiers termes d’une suite géométrique
7. On donne u_{0}=400 et q=1,78, calculer la somme des 7 premiers termes de la suite u_{n}.
S=u_0 \times \dfrac{q^{n+1}-1}{q-1}
S=400 \times \dfrac{1,78^{7+1}-1}{1,78-1}
S=400 \times \dfrac{1,78^{8}-1}{1,78-1}
S=51167,52
8. On donne u_{1}=1000 et q=0,81, calculer la somme des 10 premiers termes de la suite u_{n}.
S=u_1 \times \dfrac{q^{n}-1}{q-1}
S=1000 \times \dfrac{0,81^{10}-1}{0,81-1}
S=4623,28
Premier problème sur les suites géométriques
9. Une entreprise prévoit une augmentation de production de 7% par an. En 2017, elle produit 1000 pièces. Calculer le nombre de pièces prévue en 2024 avec le vocabulaire des suites géométriques.
augmentation :
1+t%=1+7%=1+0,07=1,07=q
u_0=1000
La production va suivre les valeurs d’une suite géométrique de premier terme u_0=1000 et de raison q=1,07
Le rang 0 correspond à l’année 2017.
L’année 2024 correspond donc au rang 7. ( si vous prenez u_1=1000 alors le rang sera 8)
On nous demande ici le nombre de pièces prévues et non la somme des pièces vendues depuis le début…on applique alors :
u_{n}=u_{0} \times q^n
u_{n}=1000 \times {1,07}^n
u_{7}=1000 \times {1,07}^7
u_{7}=1000 \times {1,07}^7
u_{7}=1605,78
L’entreprise aura une production de 1605 pièces en 2024.
Suites géométriques

SG07 – QCM : Somme des n premiers termes d’une suite géométrique

Cliquer sur le bouton « Départ » pour commencer le QCM

QCM Calcul des n premiers termes d'une suite géométriques

Départ

Félicitation - vous avez complété QCM Calcul des n premiers termes d'une suite géométriques.

Vous avez obtenu %%SCORE%% sur %%TOTAL%%.

Votre performance a été évaluée à %%RATING%%


Vos réponses sont surlignées ci-dessous.

Suites géométriques

SG06 : Somme des n premiers termes d’une suite géométrique

Pour calculer la somme des n termes d’une suite arithmétique, il faut :

  • Déterminer le nombre de termes de la suite.
  • Connaître le premier terme u_0 ou u_1 et la raison.

Appliquer l’une des formules suivantes en fonction du premier terme u_0 :

S=u_0 \times\dfrac{q^{n+1}-1}{q-1}

ou u_1 :

S=u_1 \times\dfrac{q^{n}-1}{q-1}



Exercices d’application de la formule :

1.(u_n) une suite géométrique de premier terme u_0=2 et de raison q=3. Calculer la somme des 6 premiers termes.
On utilise ici la formule avec u_0 :


S=2 \times\dfrac{3^{6+1}-1}{3-1}=2 \times\dfrac{2187-1}{3-1}=2 \times 1093= 2186
2. (v_n) une suite géométrique de premier terme v_1=3 et de raison q=2. Calculer la somme des 5 premiers termes.
On utilise ici la formule avec u_1 ou plus précisément ici v_1 :


S=3 \times\dfrac{2^{5}-1}{2-1}=3 \times\dfrac{32-1}{2-1}=3 \times 31= 93
2. (w_n) une suite géométrique de premier terme w_1=128 et de raison q=\dfrac{1}{2}. Calculer la somme des 5 premiers termes.
On utilise ici la formule avec u_1 ou plus précisément ici w_1 :


S=128 \times\dfrac{(\dfrac{1}{2})^{5}-1}{\dfrac{1}{2}-1}


S=128 \times\dfrac{0,03125-1}{-0,5}=128 \times 1,9375= 248

Suites géométriques

SG05 : Watt

Les ampoules de 40 W « classiques » étant remplacées par les ampoules LED, l’entreprise décide de diminuer sa production de 6% par mois à partir du mois de février 2017. La production prévue P_1 pour janvier 2017 est 10 000 ampoules.
1. Calculer la production P_2 pour février 2017.
Une diminution de 6% correspond à une multiplication de (1-t%) :
1-t%=1-6%=1-0,06=0,94
On multiplie donc par 0,94 la production de janvier pour connaître celle de février.
P_2=P_1 \times 0,94=10000 \times 0,94=9400
2. Calculer la production P_3 pour mars 2017.
On multiplie donc par 0,94 la production de février pour connaître celle de mars.
P_3=P_2 \times 0,94=9400 \times 0,94=8836
3. Vérifier que les productions P_1,P_2,P_3 sont les trois premiers termes d’une suite géométrique dont on déterminera la raison q.
On multiplie par 0,94 de terme en terme P_2=P_1 \times 0,94 et P_3=P_2 \times 0,94. C’est une suite géométrique de premier terme P_1=10000 et de raison q=0,94.
4. Déterminer P_n en fonction de n
On applique la formule u_n=u_1 \times q^{n-1} avec les données de la suite géométrique P_n.
P_n=P_1 \times q^{n-1}
enfin
P_n=10000 \times (0,94)^{n-1}
5. Calculer la production en décembre 2017.
Passage du mois au rang de la suite : Comme P_1 correspond au mois de janvier 2017, P_{12} correspond au mois de décembre 2017.
On applique la formule P_n=10000 \times (0,94)^{n-1} avec n=12.
P_{12}=10000 \times (0,94)^{12-1}
enfin
P_{12}=10000 \times (0,94)^{11}=4759
La production en décembre 2017 sera de 4759 ampoules.








6. L’entreprise stoppera sa production quand la production sera inférieure à 1500 ampoules. Donner la date de l’arrêt de la production.
On utilisera pour cela un tableur ou une calculatrice pour trouver le rang de la suite correspondant à une valeur de 1500 et on trouve rapidement le rang 30 correspondant juin 2019.

7. Calculer la production totale d’ampoules prévue pour l’année 2017. Arrondir à l’unité.
On applique ici la formule de la somme des 12 premiers termes d’une suite géométrique de premier terme P_1=10000 et de raison q=0,94.
S=P_1 \times \dfrac{1-q^{n}}{1-q}
S=10000 \times \dfrac{1-(0,94)^{n}}{1-0,94}
enfin pour les 12 premiers mois qui forme l’année
S=10000 \times \dfrac{1-(0,94)^{12}}{1-0,94}=87246,61
La production pour l’année 2017 sera de 87 246 ampoules.
Suites géométriques

SG04 – Problème et somme

Pour financer l’achat de cinq machines à commande numérique, l’entreprise Alpha-Usinage contracte un emprunt sur 10 ans. Chaque versement annuel augmente de 5 % par rapport au précédent. La première annuité est de 20 000 €. Le comptable de l’entreprise veut connaître le montant total du remboursement de cet emprunt.

Définition : Une annuité est une somme d’argent versée annuellement par un emprunteur pour rembourser une dette. Elle est constituée d’une partie du capital emprunté, ainsi que des intérêts dus. Elle peut être variable ou constante d’une année à l’autre.



A. Calcul des annuités

Soit u_1, u_2, …, u_{10} les montants des dix annuités.

1. Calculer le montant de la deuxième annuité u_2.
u_2=20 000+(20000 \times 5 \%)=20000+20000 \times 0,05
u_2=20000 \times 1,05
u_2=21000
2. Calculer le montant de la troisième annuité u_3.
u_3=21 000+(21000 \times 5 \%)=21000+21000 \times 0,05
u_3=21000 \times 1,05
u_3=22050
3. Calculer le montant de la quatrième annuité u_4.
u_4=22050+(22050 \times 5 \%)= 22050+22050 \times 0,05
u_4=22050 \times 1,05
u_4=23152,5
4. Calculer \dfrac{u_4}{u_3}, \dfrac{u_3}{u_2} et \dfrac{u_2}{u_1}
\dfrac{u_4}{u_3}=\dfrac{u_3}{u_2}=\dfrac{u_2}{u_1}=1,05
5. Quelle est la nature de la suite (u_n) ? Justifier et précisant la raison de cette suite.
On multiplie chaque terme par 1,05 pour trouver la valeur du terme suivant. C’est donc une suite géométrique de raison q = 1,05.








6. Exprimer u_{n} en fonction de n.
u_{n}=u_1 \times q^{n-1}
u_{n}=20000 \times 1,05^{n-1}
7. Calculer u_{10}.
On remplace n par 10 dans l’équation trouvée plus haut :
u_{10}=20000 \times 1,05^{10-1}
u_{10}=20000 \times 1,05^{9}
u_{10}=31026,56
Dans 10 ans, l’annuité sera alors de 31026,56 €.



B. Montant total du remboursement

SG4

Sur une feuille de calcul d’un tableur, reproduire la tableau représenté ci-dessus. Pour cela, saisir :

1. Quelle formule faut-il saisir dans la cellule C3 ?

C3=C2 \times 1.05
2. Compléter le tableau jusqu’à la dixième annuité.
3. Déterminer la somme à l’aide de la fonction «somme» du tableur des dix annuités.
On utilisera la fonction =somme() pour calculer la somme des 10 annuités. On trouve alors S=251557,85 en arrondissant au centième.
L’entreprise aura alors remboursée 251558 € de son emprunt au bout de 10 ans.
On verra juste après qu’une formule existe pour calculer n’importe quelle somme de n termes pour une suite géométrique.
Suites géométriques

SG03 – Cours sur les suites géométriques

Définition

Une suite géométrique est une suite de nombres qui commence par un premier nombre, le premier terme, à laquelle on multiplie toujours le même nombre q appelée raison pour ne pas confondre avec r la raison arithmétique.

Exemple :

2,4,8,16,32 est une suite géométrique de premier terme 2 et de raison 2 car on commence par 2 et on multiplie par 2 à chaque terme. 4 est le second terme,…



Notation

Pour les suites, on utilisera la notation u_n où u représente une suite (comme f représente une fonction) et n en indice est le rang de cette suite ou le classement de ce terme dans la suite.

Exemple :

u_2 représente le second terme, u_{15} le quinzième et u_n le n-ième.
On utilisera les notations suivantes :
Pour le terme précédent de le n-ième terme : u_{n-1}
Pour le terme suivant de le n-ième terme : u_{n+1}



Définition

Le terme u_n de rang n d’une suite géométrique peut être déterminé à l’aide du terme précèdent u_{n-1} et de la raison q :
u_n=u_{n-1} \times q

Définition

Le terme u_{n+1} de rang n+1 d’une suite géométrique peut être déterminé à l’aide du terme précédent u_n et de la raison q :
u_{n+1}=u_{n} \times q

Exemple :

Pour la suite 2,4,8,16,32 : u_1=2 , u_2=u_1 \times 2=4 , …



Définition :

Pour une suite géométrique de raison q, tout terme de rang n ou n-ième terme peut s’écrire de la forme :
u_{n}=u_{0} \times q^n
ou
u_{n}=u_{1} \times q^{n-1}

Entraînement :
https://www.thatquiz.org/fr-2/?-j100h-l2-mpnv600-p0

Exemple :

Pour la suite 2,4,8,16,32 de raison q=2 et u_1=2 , u_2=u_1 \times 2^{2-1}=2 \times 2^{1}=4 , … , u_5=u_1 \times 2^{5-1}=2 \times 2^{4}=32





Exercices :

Soit la suite géométrique avec comme premier terme u_0=3 et q=2.
Calculer u_1 et fonction de u_2.
Calculer u_n en fonction de n.
Calculer u_5.


Soit la suite géométrique avec comme premier terme u_1=2 et q=3.
Calculer u_2 et fonction de u_3.
Calculer u_n en fonction de n.
Calculer u_5.


Soit la suite géométrique avec comme premier terme u_1=64 et q=\dfrac{1}{4}.
Calculer u_2 et fonction de u_3.
Calculer u_n en fonction de n.
Calculer u_5.


Soit la suite géométrique avec u_3=9 et u_5=81.
En déduire q.
Calculer ensuite u_1
Calculer u_n en fonction de n.
Calculer u_6.


Soit la suite géométrique avec u_4=16 et u_6=4.
En déduire q.
Calculer ensuite u_1
Calculer u_n en fonction de n.
Calculer u_8.
Suites géométriques

SG02 : Identification de suites

Identifier les suites suivantes et trouver leur nature (arithmétique ou géométrique), leur premier terme et leur raison.


1. Soient u_0=3, u_1=9 et u_2=27.
\dfrac{u_1}{u_0}=3
\dfrac{u_2}{u_1}=3
u_3=u_2 \times 3= 81
C’est une suite géométrique de raison q=3 et de premier terme u_0=3.


2. Soient u_1=4, u_2=6 et u_3=8.
u_3-u_2=2
u_2-u_1=2
u_4=u_3+2=10
C’est une suite arithmétique de raison r=2 et de premier terme u_1=4.


3. Soient u_1=4, u_2=6 et u_3=9.
\dfrac{u_2}{u_1}=1,5
\dfrac{u_3}{u_2}=1,5
u_4=u_3 \times 1,5= 13,5
C’est une suite géométrique de raison q=1,5 et de premier terme u_1=4.


4. Soient u_0=20, u_1=15 et u_2=10.
u_2-u_1=-5
u_1-u_0=-5
u_3=u_2-5=5
C’est une suite arithmétique de raison r=-5 et de premier terme u_0=20.


5. Soient u_1=128, u_2=64 et u_3=32.
\dfrac{u_2}{u_1}=0,5
\dfrac{u_3}{u_2}=0,5
u_4=u_3 \times 0,5= 16
C’est une suite géométrique de raison q=0,5 et de premier terme u_1=128.


6. Soient u_5=64, u_2=46.
u_5=u_2+3r
r=\dfrac{64-46}{3}=6
u_1=u_2-6=40
C’est une suite arithmétique de raison r=6 et de premier terme u_1=40 ou u_0=34.


7. Soient u_4=1250, u_2=50.
u_4=u_3 \times q=u_2 \times q^2
q=\sqrt{\dfrac{1250}{50}}=\sqrt{25}=5
u_1=\dfrac{u_2}{5}=10
C’est une suite géométrique de raison q=5 et de premier terme u_1=10 ou u_0=2.


Suites géométriques

SG01 – Premier problème sur le calcul de termes d’une suite géométrique

Enoncé

On dépose un morceau de viande sur un comptoir l’été à 14h, la température avoisine les 35°C. Ce morceau de viande contient 100 bactéries, et dans ces conditions, le nombre de bactéries double toutes les 15 minutes. On note u_0 le nombre de bactéries à 14h00, u_1 le nombre de bactéries à 14h15, u_2 le nombre de bactéries à 14h30 et u_n le nombre de bactéries n quarts d’heure après 14h.


1. Quelle est la relation entre u_0 et u_1 ? puis entre u_{n} et u_{n+1} ?

u_1=u_0 \times 2
u_{n+1}=u_n \times 2
2. Préciser la nature de la suite (u_{n}) définie précédemment et sa raison.

On multiplie de terme en terme par 2. (u_n) une suite géométrique de premier terme u_0=100 et de raison 2.
3. Exprimer u_{n} en fonction de n.

u_{n}=u_0 \times q^n
u_{n}=100 \times 2^n
4. Calculer le nombre de bactéries à 17h00.

17h00 correspond à u_{12} et
u_{12}=100 \times 2^{12}
u_{12}=100 \times 2^{12}=409600
5. On estime qu’à partir de 150 000 bactéries présentes dans un aliment, celui-ci atteint un niveau impropre à la consommation pour l’être humain. Jusqu’à quelle heure, arrondie au quart d’heure, l’être humain peut-il consommer sans risque le morceau de viande ?

Il faut utiliser un tableur ou une calculatrice et vérifier à quel terme on dépasse 150 000 bactéries. Cette valeur est obtenue entre u_{10}=102400 et u_{11}=204800.
On prendra donc u_{10} qui correspond à 16h30. A 16h45, la viande sera impropre à la consommation.
Suites géométriques

SG00 : Retour aux suites arithmétiques

Jouons aux allumettes
SG-0
1.Compter le nombre d’allumettes à ajouter à chaque construction pour obtenir un étage de plus.
– pour le premier étage : u_1
u_1=3
– pour le deuxième étage : u_2
u_2=7
– pour le troisième étage : u_3
u_3=11
– pour le quatrième étage : u_4
u_4=15
2.Montrer que u_1;u_2;u_3 et u_4 forment une suite arithmétique de raison r=4.
u_4-u_3=u_3-u_2=u_2-u_1=4
3.En déduire le nombre d’allumettes nécessaires à ajouter pour passer du quatrième au cinquième étage.
u_5=u_4+4=15+4=19
Il faut ajouter 19 allumettes pour passer du quatrième au cinquième étage.
Ecrire la formule qui permet le calcul direct de u_5 en fonction de u_1 et r.
u_5=u_1+4 \times r
Ecrire la relation entre u_n et n.
u_n=u_1+(n-1) \times r
u_n=3+(n-1) \times 4
u_n=4n-1
Combien d’allumettes au total pour couvrir les cinq étages.
Il faut utiliser la formule de la somme des premiers termes d’une suite arithmétique.
S=\dfrac{n(u_1+u_n)}{2}
S=\dfrac{5(u_1+u_5)}{2}
S=\dfrac{5(3+19)}{2}
S=55
La boîte d’allumettes contient 300 allumettes.Déterminer le nombre d’étages qu’Aline pourra construire.
S=\dfrac{n(u_1+u_n)}{2}
300=\dfrac{n(3+u_n)}{2}
300=\dfrac{n(3+4n-1)}{2}
300=\dfrac{n(4n+2)}{2}
300=n(2n+1)
300=2n^2+n
2n^2+n-300=0
Résolution d’une équation du second degré à une inconnue.

Suites arithmétiques

SA-07 : Activé 2 – Calcul de la somme des termes d’une suite arithmétique

L’entreprise LocaMat est spécialisée dans la location d’engins et de matériel de chantier. Stéphane souhaite louer une mini-pelle hydraulique. Il consulte donc le site internet de l’entreprise. Pour la location de la mini-pelle, l’entreprise pratique des tarifs dégressifs suivant la durée de location. Par souci d’économie, il se demande quelle formule choisir.

A. Location à la semaine

En naviguant dans la rubrique des différentes offres commerciales de LocaMat, Stéphane trouve d’abord la proposition ci-contre : le forfait Loca-semaine.
forfait loca-semaine
1. Soit u_1=70 le prix à payer pour une journée de location. A l’aide de la calculatrice, calculer u_2, u_3 et u_4.







2. Quelle est la nature de cette suite ? Préciser sa raison.







3. Ecrire u_n en fonction de n.







4. Calculer u_7.



Calcul de la somme des n premiers termes d’une suite arithmétique
somme arith
5. En utilisant la méthode ci-dessus, déterminer la somme totale à payer pour une location de 7 jours.







B. Location au mois

Toujours sur le site de LocaMat, Stéphane consulte ensuite les tarifs réservés aux professionnels et découvre le forfait Loca-mensuel ci-après.
forfait loca-mois
On note v_1 le prix à payer pour une journée de location, v_2 celui de la deuxième journée, etc.
Soit v_1=87 le prix à payer pour une première journée de location.
1. Quelle est la nature de cette suite v_n ? Préciser sa raison.



2. Ecrire v_n en fonction de n.







3. Calculer le prix du 7ème jour et du 28ème jour.







4. Calculer la somme totale pour 7 jours de location puis pour 28 jours de location.







Suites arithmétiques

SA-06 : Exercice de recherche de la valeur de n

Exercice 05 : Comme des sardines

En 2008, l’entreprise « Fabriq » a produit 63200 boîtes de sardine.
Sa production a augmenté de 1300 boîtes de sardine chaque année.
1. Déterminer la production en 2009,en 2010 et en 2011.







2. Quelle est la nature de la suite de productions (u_n)? Justifier.







3. Déterminer son premier terme et sa raison.



4. Ecrire u_n en fonction de n.





5. Calculer la production en 2015.



6. L’entreprise a une capacité de production maximale annuelle de 84000 boîtes de sardine. En supposant que la production continue d’augmenter de 1300 unités par an, déterminer l’année où la production attendra son maximum.